题目内容
如图,已知正方体ABCD—A1B1C1D1中,E、F分别为D1C1、B1C1的中点,AC∩BD=P,A1C1∩EF=Q.求证:
(1)D、B、F、E四点共面;
(2)若A1C交平面DBEF于R点,则P、Q、R三点共线.
证明:(1)∵EF是△D1B1C1的中位线,∴EF∥B1D1.?
在正方体ABCD—A1B1C1D1中,B1D1![]() BD,∴EF∥BD.?
BD,∴EF∥BD.?
?∴EF、BD确定一个平面,即D、B、F、E四点共面.?
(2)正方体ABCD—A1B1C1D1中,设A1ACC1确定的平面为α,又设平面BDEF为β,∵Q∈A1C1,∴Q∈α.?
又Q∈EF,∴Q∈β.?
则Q是α与β的公共点,同理,P点也是α和β的公共点,∴α∩β=PQ.?
又A1C∩β=R,∴R∈A1C.?
∴R∈α且R∈β.则R∈PQ.?
故P、Q、R三点共线.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )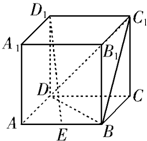 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.