Question

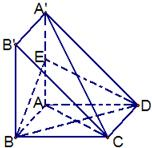如图，四边形ABCD与A'ABB'都是边长为a的正方形，点E是A'A的中点，A'A⊥平面ABCD
（1）求证：A'C∥平面BDE；
（2）求证：平面A'AC⊥平面BDE
（3）求体积V_A'-ABCD与V_E-ABD的比值．

Answer 1

分析：（1）设BD交AC于M，连接ME．由三角形的中位线定理可得ME∥A'C，结合线面平行的判定定理，即可得到A'C∥平面BDE；
（2）根据已知条件，得到BD⊥AC，A'A⊥BD．由线面垂直的判定定理可得BD⊥平面A'AC，再由面面垂直的判定定理，可得平面A'AC⊥平面BDE
（3）棱锥A'-ABCD与棱锥E-ABD的底面面积之比为2：1，高之比也为2：1，代入棱锥体积公式，即可求出体积V_A'-ABCD与V_E-ABD的比值．

解答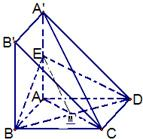：证明：（1）设BD交AC于M，连接ME．∵ABCD为正方形，所以M为AC中点，
又∵E为A'A的中点∴ME为△A'AC的中位线∴ME∥A'C
又∵ME?平面BDE，A'C?平面BDE∴A'C∥平面BDE．                        …（4分）
（2）∵ABCD为正方形∴BD⊥AC…（6分）
∵A'A⊥平面ABCD，BD?平面ABCD
∴A'A⊥BD．
又AC∩A'A=A
∴BD⊥平面A'AC．
∵BD?平面BDE
∴平面A'AC⊥平面BDE…（8分）
解：（3）V_A'-ABCD：V_E-ABD=4：1…（12分）

点评：本题考查的知识点是平面与平面垂直的判定，棱锥的体积，直线与平面平行的判定，熟练掌握空间中直线与平面平行或垂直的判定、性质、定义、几何特征及棱锥的体积公式是解答本题的关键．