题目内容
已知二次函数f(x)满足条件f(0)=1,及f(x+1)-f(x)=2x.(1)求函数f(x)的解析式;
(2)求函数f(x)在[a,a+1](a∈R)上的最小值g(a)的表达式.
【答案】分析:(1)设出二次函数的解析式,根据f(0)=1,及f(x+1)-f(x)=2x结合多项式相等的条件,构造方程,可求出待定系数,得到函数f(x)的解析式;
(2)根据(1)中函数的解析式,结合二次函数的图象和性质,讨论区间[a,a+1]与对称轴的位置关系,可求出函数f(x)在[a,a+1](a∈R)上的最小值g(a)的表达式.
解答:解:(1)∵二次函数f(x)满足条件f(0)=1,
∴设f(x)=ax2+bx+1,
则f(x+1)-f(x)=a(x+1)2+b(x+1)-ax2-bx=2ax+a+b=2x
∴2a=2,a+b=0,
则a=1,b=-1,
所以f(x)=x2-x+1
(2)f(x)=x2-x+1=(x- )2-
)2-
当a+1≤ ,即a≤-
,即a≤- 时,函数f(x)在[a,a+1]上是单调减函数,
时,函数f(x)在[a,a+1]上是单调减函数,
则g(a)=f(a+1)=a2+a+1
当a< <a+1,即-
<a+1,即- <a<
<a< 时,则g(a)=f(
时,则g(a)=f( )=
)=
当a≥ 时,函数f(x)在[a,a+1]上是单调增函数,则g(a)=f(a)=a2-a+1
时,函数f(x)在[a,a+1]上是单调增函数,则g(a)=f(a)=a2-a+1
综上:g(a)=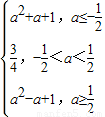
点评:本题考查的知识点是二次函数在闭区间上的最值,函数的解析式的求法--待定系数法,熟练掌握二次函数的图象和性质是解答的关键.
(2)根据(1)中函数的解析式,结合二次函数的图象和性质,讨论区间[a,a+1]与对称轴的位置关系,可求出函数f(x)在[a,a+1](a∈R)上的最小值g(a)的表达式.
解答:解:(1)∵二次函数f(x)满足条件f(0)=1,
∴设f(x)=ax2+bx+1,
则f(x+1)-f(x)=a(x+1)2+b(x+1)-ax2-bx=2ax+a+b=2x
∴2a=2,a+b=0,
则a=1,b=-1,
所以f(x)=x2-x+1
(2)f(x)=x2-x+1=(x-
 )2-
)2-
当a+1≤
 ,即a≤-
,即a≤- 时,函数f(x)在[a,a+1]上是单调减函数,
时,函数f(x)在[a,a+1]上是单调减函数,则g(a)=f(a+1)=a2+a+1
当a<
 <a+1,即-
<a+1,即- <a<
<a< 时,则g(a)=f(
时,则g(a)=f( )=
)=
当a≥
 时,函数f(x)在[a,a+1]上是单调增函数,则g(a)=f(a)=a2-a+1
时,函数f(x)在[a,a+1]上是单调增函数,则g(a)=f(a)=a2-a+1综上:g(a)=
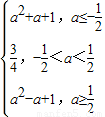
点评:本题考查的知识点是二次函数在闭区间上的最值,函数的解析式的求法--待定系数法,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目