题目内容
已知、B、C分别为△ABC的三边a、b、c所对的角，向量
=(sinA，sinB)，
=（cosB，-cosA）且
•
=2C．
（Ⅰ）求角C的大小；
（Ⅱ）若sinA，sinC，sinB成等差数列，且
•(
-
)=18，求边c的长．
| m |
| n |
| m |
| n |
（Ⅰ）求角C的大小；
（Ⅱ）若sinA，sinC，sinB成等差数列，且
| CA |
| AB |
| AC |
（Ⅰ）
•
=sinA•cosB+sinB•cosA=sin(A+B)
在△ABC中，由于sin（A+B）=sinC，∴
•
=sinC.
又∵
•
=sin2C，∴sin2C=sinC，2sinCcosC=sinC
又sinC≠0，所以cosC=
，而0＜C＜π，因此C=
．
（Ⅱ）由sinA，sinC，sinB成等差数列，得2sinC=sinA+sinB，
由正弦定理得2c=a+b．
∵
•(
-
)=18，∴
•
=18，
即abcosC=18，由（Ⅰ）知cosC=
，所以ab=36．
由余弦弦定理得c2=a2+b2-2abcosC=（a+b）2-3ab，
∴c2=4c2-3×36，
∴c2=36，
∴c=6．
| m |
| n |
在△ABC中，由于sin（A+B）=sinC，∴
| m |
| n |
又∵
| m |
| n |
又sinC≠0，所以cosC=
| 1 |
| 2 |
| π |
| 3 |
（Ⅱ）由sinA，sinC，sinB成等差数列，得2sinC=sinA+sinB，
由正弦定理得2c=a+b．
∵
| CA |
| AB |
| AC |
| CA |
| CB |
即abcosC=18，由（Ⅰ）知cosC=
| 1 |
| 2 |
由余弦弦定理得c2=a2+b2-2abcosC=（a+b）2-3ab，
∴c2=4c2-3×36，
∴c2=36，
∴c=6．
练习册系列答案
相关题目
，
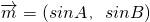=（cosB，-cosA）且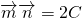
．
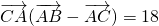，求边c的长．
，
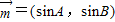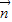=（cosB，-cosA）且
．
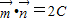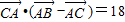，求边c的长．
，
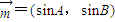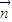=（cosB，-cosA）且
．
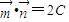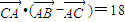，求边c的长．