Question

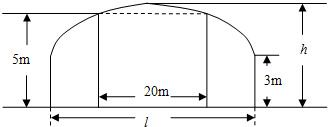
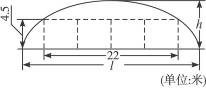
如图,某隧道设计为双向四车道，车道总宽22 m，要求通行车辆限高4.5 m，隧道全长2.5 km，隧道的拱线近似地看成半个椭圆形状.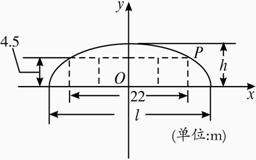

（1）若最大拱高h为6 m，则隧道设计的拱宽l是多少？

（2）若最大拱高h不小于6 m，则应如何设计拱高h和拱宽l，才能使半个椭圆形隧道的土方工程量最小？（半个椭圆的面积公式为lh，柱体体积为底面积乘以高.结果精确到0.1 m）

Answer 1

解析:当最大拱高h为定值时,隧道设计的拱宽l即为2a；当最大拱高h为变量时,可根据均值定理,得到椭圆面积为最小.

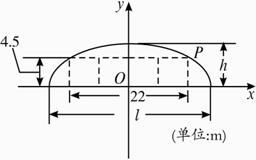
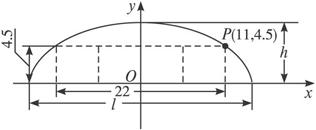
解:（1）如图建立坐标系,则点P(11,4.5),椭圆方程为=1.将b=h=6与点P坐标代入椭圆方程,得a=,l=2a=≈33.3.故隧道的拱宽约为33.3 m.?

（2）由椭圆方程=1,得=1.?

因为≥

即ab≥99,且l=2a,h=b,?

所以S=lh=≥.?

当S取最小值时,有,得a=11,b=,此时,l=2a=22≈31.1,h=b≈6.4.?

故当拱高约为6.4 m,拱宽约为31.1 m时,土方工程量最小.