Question

已知，b，c为△ABC的三个内角A，B，C的对边，向量m =（），
n＝（cosA,sinA）.若，且，则角＝        .

Answer 1

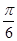
解析试题分析：根据题意，，所以=0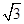，cosA-sinA=0，A=；
由正弦定理可得，sinAcosB+sinBcosA=sinCsinC，
又由sinAcosB+sinBcosA=sin（A+B）=sinC，
化简可得，sinC=sin²C，
则C=，则 B=。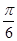
考点：本题主要考查平面向量的坐标运算，向量垂直的条件，两角和与差的三角函数，正弦定理。
点评：典型题，本题具有一定综合性，较全面地考查了向量、三角、正弦定理等基础知识。难度不大。