题目内容
下列四组函数中,表示同一函数的是( )A.f(x)=
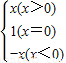 ,g(x)=
,g(x)=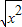
B.f(x)=lgx2,g(x)=2lg
C.f(x)=sin(2x+
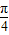 ),g(x)=cos(2x-
),g(x)=cos(2x-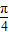 )
)D.f(x)=
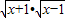 ,g(x)=
,g(x)=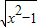
【答案】分析:分别判断两个函数的定义域和对应法则是否完全相同即可.
解答:解:A.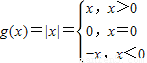 ,当x=0时的对应法则不相同,所以f(x),g(x)不能表示同一函数.
,当x=0时的对应法则不相同,所以f(x),g(x)不能表示同一函数.
B.f(x)=lgx2,的定义域为{x|x≠0},g(x)=2lgx的定义域为{x|x>0},所以两个函数的定义域不同,所以f(x),g(x)不能表示同一函数.
C.两个函数的定义域都为R,f(x)=sin(2x+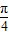 )=
)=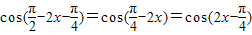 ,所以f(x),g(x)能表示同一函数.
,所以f(x),g(x)能表示同一函数.
D.要使函数f(x)有意义,则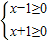 ,即x≥1,要使函数g(x)有意义,则x2-1≥0,解得x≤-1或x≥1,所以两个函数的定义域不同,所以f(x),g(x)不能表示同一函数.
,即x≥1,要使函数g(x)有意义,则x2-1≥0,解得x≤-1或x≥1,所以两个函数的定义域不同,所以f(x),g(x)不能表示同一函数.
故选C.
点评:本题主要考查判断两个函数是否为同一函数,判断的标准是函数的定义域与对应法则是否完全相同.
解答:解:A.
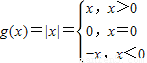 ,当x=0时的对应法则不相同,所以f(x),g(x)不能表示同一函数.
,当x=0时的对应法则不相同,所以f(x),g(x)不能表示同一函数.B.f(x)=lgx2,的定义域为{x|x≠0},g(x)=2lgx的定义域为{x|x>0},所以两个函数的定义域不同,所以f(x),g(x)不能表示同一函数.
C.两个函数的定义域都为R,f(x)=sin(2x+
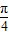 )=
)=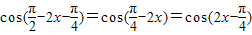 ,所以f(x),g(x)能表示同一函数.
,所以f(x),g(x)能表示同一函数.D.要使函数f(x)有意义,则
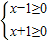 ,即x≥1,要使函数g(x)有意义,则x2-1≥0,解得x≤-1或x≥1,所以两个函数的定义域不同,所以f(x),g(x)不能表示同一函数.
,即x≥1,要使函数g(x)有意义,则x2-1≥0,解得x≤-1或x≥1,所以两个函数的定义域不同,所以f(x),g(x)不能表示同一函数.故选C.
点评:本题主要考查判断两个函数是否为同一函数,判断的标准是函数的定义域与对应法则是否完全相同.

练习册系列答案
相关题目
下列四组函数中,表示相等函数的一组是( )
A、f(x)=|x|,g(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
下列四组函数中,表示相等函数的一组是( )
A、f(x)=|x-1|,g(x)=
| ||||||
B、f(x)=(
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
下列四组函数中,表示同一个函数的是( )
A、f(x)=|x+1|,g(x)=
| ||||
B、f(x)=
| ||||
C、f(x)=
| ||||
| D、f(x)=2 log2x,g(x)=x |