题目内容
已知a,b∈R+,下列不等式:①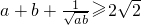 ,②
,②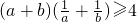 ,③
,③ ,④
,④ ,其中一定恒成立的是________(填写序号).
,其中一定恒成立的是________(填写序号).
①②③
分析:利用a+b≥ 证明①正确;把左边展开后再用基本不等式进行证明②正确;利用平方后作差、变形和判断符号证明③正确;把a+b≥
证明①正确;把左边展开后再用基本不等式进行证明②正确;利用平方后作差、变形和判断符号证明③正确;把a+b≥ 取倒数后,再两边同乘以2ab证明出④不正确.
取倒数后,再两边同乘以2ab证明出④不正确.
解答:由于a,b∈R+,则
①、∵a+b≥ ,当且仅当a=b时取等号,∴
,当且仅当a=b时取等号,∴
 成立,故①正确;
成立,故①正确;
②、 =2+
=2+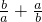 ≥4,当且仅当
≥4,当且仅当 时取等号,故②正确;
时取等号,故②正确;
③、∵ =
= [a4+b4+2a2b2-ab(a+b)2]
[a4+b4+2a2b2-ab(a+b)2]
= =
= =
=
= ≥0,∴
≥0,∴ ,故③正确;
,故③正确;
④、∵a+b≥ ,当且仅当a=b时取等号,∴
,当且仅当a=b时取等号,∴ ,故④不对;
,故④不对;
故答案为:①②③.
点评:本题考查了基本不等式的应用,结合做差法以及两边平方后再作差,后不等式取倒数等进行证明,注意:“一正、二定、三相等”的说明.
分析:利用a+b≥
 证明①正确;把左边展开后再用基本不等式进行证明②正确;利用平方后作差、变形和判断符号证明③正确;把a+b≥
证明①正确;把左边展开后再用基本不等式进行证明②正确;利用平方后作差、变形和判断符号证明③正确;把a+b≥ 取倒数后,再两边同乘以2ab证明出④不正确.
取倒数后,再两边同乘以2ab证明出④不正确.解答:由于a,b∈R+,则
①、∵a+b≥
 ,当且仅当a=b时取等号,∴
,当且仅当a=b时取等号,∴
 成立,故①正确;
成立,故①正确;②、
 =2+
=2+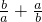 ≥4,当且仅当
≥4,当且仅当 时取等号,故②正确;
时取等号,故②正确;③、∵
 =
= [a4+b4+2a2b2-ab(a+b)2]
[a4+b4+2a2b2-ab(a+b)2]=
 =
= =
=
=
 ≥0,∴
≥0,∴ ,故③正确;
,故③正确;④、∵a+b≥
 ,当且仅当a=b时取等号,∴
,当且仅当a=b时取等号,∴ ,故④不对;
,故④不对;故答案为:①②③.
点评:本题考查了基本不等式的应用,结合做差法以及两边平方后再作差,后不等式取倒数等进行证明,注意:“一正、二定、三相等”的说明.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目