题目内容
（2004•朝阳区一模）已知sinα-sinβ=-
，cosα-cosβ=
，且α、β均为锐角，则cos（α-β）=
，ctg（α-β）=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
-
3
| ||
| 7 |
-
．3
| ||
| 7 |
分析：两式平方相加可求cos（α-β），利用平方关系及商数关系，可求ctg（α-β）的值．
解答：解：两式平方相加可得：2-2cos（α-β）=
，∴cos（α-β）=
∵α、β均为锐角，α＜β，
∴sin（α-β）=-
∴ctg（α-β）=
=
=-
故答案为：
，-
| 1 |
| 2 |
| 3 |
| 4 |
∵α、β均为锐角，α＜β，
∴sin（α-β）=-
| ||
| 4 |
∴ctg（α-β）=
| cos(α-β) |
| sin(α-β) |
| ||||
-
|
3
| ||
| 7 |
故答案为：
| 3 |
| 4 |
3
| ||
| 7 |
点评：本题考查同角三角函数的关系，考查学生的计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
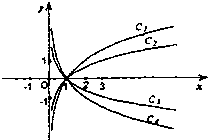（2004•朝阳区一模）已知图中曲线C1、C2、C3、C4是函数logax的图象，则曲线C1、C2、C3、C4对应的a的值依次为（ ）