题目内容
(2012•通州区一模)已知椭圆C的焦点在y轴上,离心率为
,且短轴的一个端点到下焦点F的距离是
.
(I)求椭圆C的标准方程;
(II)设直线y=-2与y轴交于点P,过点F的直线l交椭圆C于A,B两点,求△PAB面积的最大值.
| ||
| 2 |
| 2 |
(I)求椭圆C的标准方程;
(II)设直线y=-2与y轴交于点P,过点F的直线l交椭圆C于A,B两点,求△PAB面积的最大值.
分析:(Ⅰ)设椭圆C的方程,利用短轴的一个端点到下焦点F的距离是
,离心率为
,可求椭圆C的标准方程;
(Ⅱ)由(Ⅰ)知F(0,-1),P(0,-2),且直线l的斜率存在,设其方程代入椭圆方程,从而可表示△PAB面积,利用基本不等式,即可求得△PAB面积的最大值.
| 2 |
| ||
| 2 |
(Ⅱ)由(Ⅰ)知F(0,-1),P(0,-2),且直线l的斜率存在,设其方程代入椭圆方程,从而可表示△PAB面积,利用基本不等式,即可求得△PAB面积的最大值.
解答:解:(Ⅰ)因为椭圆C的焦点在y轴上,所以设椭圆C的方程是
+
=1(a>b>0).…(1分)
因为短轴的一个端点到下焦点F的距离是
,离心率为
所以a=
,c=1
所以b2=a2-c2=1
所以椭圆C的标准方程是
+x2=1 …(4分)
(Ⅱ)由(Ⅰ)知F(0,-1),P(0,-2),且直线l的斜率存在,
设其方程为:y=kx-1,代入椭圆方程可得(2+k2)x2-2kx-1=0…(6分)
设A(x1,y1),B(x2,y2),所以x1+x2=
,x1x2=
.…(7分)
所以△PAB面积S△PAB=
|PF||x1-x2|(x1,x2异号).
所以S△PAB=
=
≤
…(12分)
当且仅当1+k2=
,即k=0时,S△PAB有最大值是
所以当k=0时,△PAB面积的最大值是
…(13分)
| y2 |
| a2 |
| x2 |
| b2 |
因为短轴的一个端点到下焦点F的距离是
| 2 |
| ||
| 2 |
所以a=
| 2 |
所以b2=a2-c2=1
所以椭圆C的标准方程是
| y2 |
| 2 |
(Ⅱ)由(Ⅰ)知F(0,-1),P(0,-2),且直线l的斜率存在,
设其方程为:y=kx-1,代入椭圆方程可得(2+k2)x2-2kx-1=0…(6分)
设A(x1,y1),B(x2,y2),所以x1+x2=
| 2k |
| 2+k2 |
| -1 |
| 2+k2 |
所以△PAB面积S△PAB=
| 1 |
| 2 |
所以S△PAB=
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
|
| ||
| 2 |
当且仅当1+k2=
| 1 |
| 1+k2 |
| ||
| 2 |
所以当k=0时,△PAB面积的最大值是
| ||
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
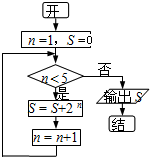 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )