题目内容
在等差数列{an}中,Sn为其前n项和(n∈N*),且a3=5,S3=9.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设
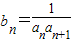 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】分析:(Ⅰ)依题意,解方程组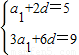 可求得a1与d,从而可求等差数列{an}的通项公式;
可求得a1与d,从而可求等差数列{an}的通项公式;
(Ⅱ)利用裂项法可求得bn= (
(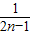 -
-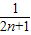 ),从而可求数列{bn}的前n项和Tn.
),从而可求数列{bn}的前n项和Tn.
解答:解:(Ⅰ)由已知条件得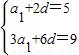 …(2分)
…(2分)
解得a1=1,d=2,…(4分)
∴an=2n-1.…(6分)
(Ⅱ)由(Ⅰ)知,an=2n-1,
∴bn=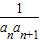 =
=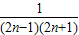 =
= (
(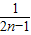 -
-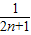 ),…(9分)
),…(9分)
∴Tn=b1+b2+…+bn= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(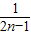 -
-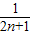 )]
)]
= (1-
(1-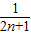 )
)
=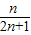 .…(12分)
.…(12分)
点评:本题考查等差数列的通项公式,着重考查裂项法求和,求得bn= (
(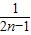 -
-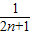 )是关键,属于中档题.
)是关键,属于中档题.
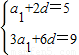 可求得a1与d,从而可求等差数列{an}的通项公式;
可求得a1与d,从而可求等差数列{an}的通项公式;(Ⅱ)利用裂项法可求得bn=
 (
(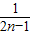 -
-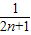 ),从而可求数列{bn}的前n项和Tn.
),从而可求数列{bn}的前n项和Tn.解答:解:(Ⅰ)由已知条件得
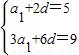 …(2分)
…(2分)解得a1=1,d=2,…(4分)
∴an=2n-1.…(6分)
(Ⅱ)由(Ⅰ)知,an=2n-1,
∴bn=
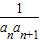 =
=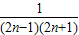 =
= (
(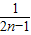 -
-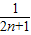 ),…(9分)
),…(9分)∴Tn=b1+b2+…+bn=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(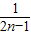 -
-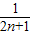 )]
)]=
 (1-
(1-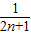 )
)=
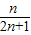 .…(12分)
.…(12分)点评:本题考查等差数列的通项公式,着重考查裂项法求和,求得bn=
 (
(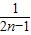 -
-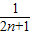 )是关键,属于中档题.
)是关键,属于中档题. 
练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目