Question

设数列{a_n}满足a₁＝a，a_n＋1＝a_n²＋a₁，．

(1)当a∈（－∞，－2）时，求证：M；(2)当a∈（0，］时，求证：a∈M；

(3)当a∈（，＋∞）时，判断元素a与集合M的关系，并证明你的结论．

Answer 1

证明：（1）如果，则，． ………………………………………2分

（2） 当 时，（）．

          事实上，〔〕当时，．

设时成立（为某整数），

则〔〕对，．

由归纳假设，对任意n∈N^*，|a_n|≤＜2，所以a∈M．…………………………6分

 （3） 当时，．证明如下：

对于任意，，且．

对于任意，，

则．

 所以，．

当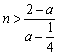时，，即，因此．…10分