题目内容
 如图,直线l过点P(4,1),交x轴、y轴正半轴于A、B两点;
如图,直线l过点P(4,1),交x轴、y轴正半轴于A、B两点;(1)求△AOB面积的最小值及此时直线l的方程;
(2)已知直线l1:y=kx+3k+3(k∈R)经过定点D,当点M(m,n)在线段DP上移动时,求
| n+2 |
| m+1 |
(3)求
| PA |
| PB |
分析:(1)由题意设所求直线方程为
+
=1,可得
+
=1,由基本不等式可得ab的最小值,进而可得答案;
(2)可得直线l1过定点D(-3,3),
表示线段DP上的点与Q(-1,-2)连线的斜率,数形结合可得;
(3)可得
=(a-4,-1),
=(-4,b-1),进而可得
•
=-(4a+b)(
+
)+17,由基本不等式可得.
| x |
| a |
| y |
| b |
| 4 |
| a |
| 1 |
| b |
(2)可得直线l1过定点D(-3,3),
| n+2 |
| m+1 |
(3)可得
| PA |
| PB |
| PA |
| PB |
| 4 |
| a |
| 1 |
| b |
解答:解:(1)由题意设所求直线方程为
+
=1,(a>0,b>0)
则A(a,0),B(0,b)
∵直线l过点P(4,1),∴
+
=1,
由基本不等式可得1=
+
≥2
,
变形可得ab≥16,当且仅当
=
即a=8,b=2时取等号
∴△AOB面积S=
ab≥
×16=8,
∴△AOB面积的最小值为8,此时直线l的方程为
+
=1,即x+4y-8=0
(2)直线l1:y=kx+3k+3可化为y-3=k(x+3),
由点斜式可知直线过定点D(-3,3),
表示线段DP上的点与Q(-1,-2)连线的斜率,
由又可得DQ的斜率为
=-
,PQ的斜率为
=
数形结合可得
的取值范围为[
,+∞)∪(-∞,-
];
(3)由(1)可得
=(a-4,-1),
=(-4,b-1),
∴
•
=-4(a-4)-(b-1)=-4a-b+17=-(4a+b)(
+
)+17
=-(17+
+
)+17≤-(17+2
)+17=-8,
当且仅当
=
,即a=b=5时取等号,
∴
•
的最大值为-8,此时直线l的方程为x+y-5=0
| x |
| a |
| y |
| b |
则A(a,0),B(0,b)
∵直线l过点P(4,1),∴
| 4 |
| a |
| 1 |
| b |
由基本不等式可得1=
| 4 |
| a |
| 1 |
| b |
|
变形可得ab≥16,当且仅当
| 4 |
| a |
| 1 |
| b |
∴△AOB面积S=
| 1 |
| 2 |
| 1 |
| 2 |
∴△AOB面积的最小值为8,此时直线l的方程为
| x |
| 8 |
| y |
| 2 |
(2)直线l1:y=kx+3k+3可化为y-3=k(x+3),
由点斜式可知直线过定点D(-3,3),
| n+2 |
| m+1 |
由又可得DQ的斜率为
| 3-(-2) |
| -3-(-1) |
| 5 |
| 2 |
| -2-1 |
| -1-4 |
| 3 |
| 5 |
数形结合可得
| n+2 |
| m+1 |
| 3 |
| 5 |
| 5 |
| 2 |
(3)由(1)可得
| PA |
| PB |
∴
| PA |
| PB |
| 4 |
| a |
| 1 |
| b |
=-(17+
| 4b |
| a |
| 4a |
| b |
|
当且仅当
| 4b |
| a |
| 4a |
| b |
∴
| PA |
| PB |
点评:本题考查平面向量数量积的运算,涉及直线的斜率与基本不等式,以及数形结合的思想,属中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
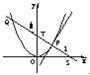 如图,P是抛物线C:y=
如图,P是抛物线C:y=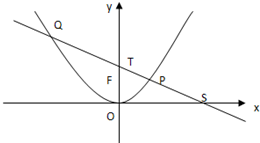 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2). 如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.
如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.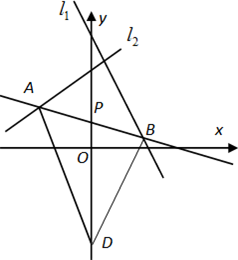 如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.
如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.