题目内容
如图,在三棱锥 中,
中, ,且
,且 ,
, 平面
平面 ,过
,过 作截面分别交
作截面分别交 于
于 ,且二面角
,且二面角 的大小为
的大小为 ,则截面
,则截面 面积的最小值为 .
面积的最小值为 .
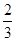
解析试题分析:过P做PG⊥EF,垂足为G,连接CG则由三垂线定理可得EF⊥CG,∴∠PGC即为二面角角P-EF-C的平面角,
∴∠PGC=60°,PC=1,∴在三角形PEF斜边EF边上的高为PG= ,CG=
,CG= ,设CE=a,CF=b,则EF=
,设CE=a,CF=b,则EF= ,在三角形CEF中,ab=
,在三角形CEF中,ab= ×
× ,又
,又 ,∴ab≥
,∴ab≥ ,∴
,∴ ,∴三角形PEF的面积为
,∴三角形PEF的面积为 ,故截面
,故截面 面积的最小值为
面积的最小值为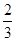
考点:本题考查了二面角的应用.
点评:解决此类问题的关键是利用三垂线定理作出二面角,然后利用基本不等式求出最值即可

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, 为
为 的中点,点
的中点,点 为侧面
为侧面 内一动点(含边界),若动点
内一动点(含边界),若动点 ,则动点
,则动点 的棱长为2,则异面直线
的棱长为2,则异面直线 与AC之间的距离为_________。
与AC之间的距离为_________。 异面的有__________条
异面的有__________条 平面
平面 ;②
;② 平面
平面 ;③平面
;③平面
 平面
平面 ;④平面
;④平面
 .以上四个命题中,正确命题的序号是 。
.以上四个命题中,正确命题的序号是 。
 、
、 是直线,
是直线, 、
、 是平面,
是平面, ,向量
,向量 在
在 在
在 ,
,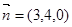 ,则
,则 的底面是边长为1的正方形,侧棱长
的底面是边长为1的正方形,侧棱长 ,则异面直线
,则异面直线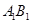 与
与 的夹角大小等于___________.
的夹角大小等于___________.