题目内容
已知![]() 是定义在
是定义在![]() 上的函数,
上的函数,![]() ,且
,且![]()
![]() ,总有
,总有
![]() 恒成立.
恒成立.
(Ⅰ)求证:![]() 是奇函数;
是奇函数;
(Ⅱ)对![]()
![]() ,有
,有![]() ,
,![]() ,求:
,求:
![]() 及
及![]() ;
;
(Ⅲ)求![]()
![]() 的最小值.
的最小值.
解:⑴证明:![]() ,
,
令![]() 得
得![]() ,再令
,再令![]() ,得
,得![]()
![]() ,函数
,函数![]() 是奇函数.
是奇函数.
⑵令![]() 得
得![]() ,所以
,所以![]() ,
,![]() ,
,
![]() ,
,![]()
![]()
又![]() ,
,![]() ①
①
![]() ②
②
由①-②得![]()
⑶![]()
![]() .
.
又![]() ,
,![]()
![]() 的最小值为
的最小值为![]()
w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
![]() 高☆考♂资♀源/span>
高☆考♂资♀源/span>
w.w.w.k.s.5.u.c.o.m



 www.ks5u.com
www.ks5u.com

练习册系列答案
相关题目
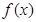 是定义在
是定义在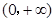 上的单调函数,且对任意的
上的单调函数,且对任意的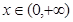 ,都有
,都有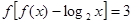 ,则方程
,则方程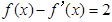 的解所在的区间是
( )
的解所在的区间是
( )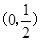
 B.
B.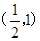 C.
C.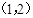 D.
D.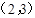
 是定义在
是定义在 上的奇函数,且满足
上的奇函数,且满足 ,则f(2011)= ;
,则f(2011)= ;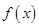 是定义在
是定义在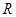 上的可导函数,对任意
上的可导函数,对任意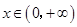 ,都有
,都有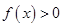 ,且
,且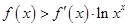 ,则
,则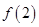 与
与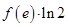 的大小关系是 ( )
的大小关系是 ( )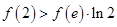 B.
B.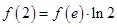
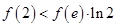 D.不能确定
D.不能确定 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,那么
,那么 的值是( )
的值是( ) B、
B、 C、
C、 D、
D、