题目内容
已知函数f(x)=lnx+a
,其中a为大于零的常数.
(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证：对于任意的n∈N*,且n>1时,都有lnn>
+
+…+
恒成立.
,其中a为大于零的常数.(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证：对于任意的n∈N*,且n>1时,都有lnn>
++…+恒成立. （1）(0,1] （2）见解析
(1)f′(x)=
(x>0),
由已知,得f′(x)≥0在[1,+∞)上恒成立,即a≤x在[1,+∞)上恒成立,又因为当x∈[1,+∞)时,x≥1,
所以a≤1,即a的取值范围为(0,1].
(2)由(1)知函数f(x)=lnx+
-1在[1,+∞)上为增函数,
当n>1时,因为
>1,所以f
>f(1),
即lnn-ln(n-1)>,对于n∈N*,且n>1恒成立,
lnn=[lnn-ln(n-1)]+[ln(n-1)-ln(n-2)]+…+[ln3-ln2]+[ln2-ln 1]>+
+…++,所以对于n∈N*,且n>1时,lnn>++…+恒成立.
(x>0),由已知,得f′(x)≥0在[1,+∞)上恒成立,即a≤x在[1,+∞)上恒成立,又因为当x∈[1,+∞)时,x≥1,
所以a≤1,即a的取值范围为(0,1].
(2)由(1)知函数f(x)=lnx+
-1在[1,+∞)上为增函数,当n>1时,因为
>1,所以f>f(1),即lnn-ln(n-1)>
,对于n∈N*,且n>1恒成立,lnn=[lnn-ln(n-1)]+[ln(n-1)-ln(n-2)]+…+[ln3-ln2]+[ln2-ln 1]>
++…++,所以对于n∈N*,且n>1时,lnn>++…+恒成立.
练习册系列答案
名校课堂系列答案
相关题目
，g(x)＝f(x)－ax，x∈[1,3]，其中a∈R，记函数g(x)的最大值与最小值的差为h(a)．
为偶函数．
的值；
有且只有一个根，求实数
的取值范围．
上的一个映射，正整数数对
在映射f下的象为实数z，记作
. 对于任意的正整数
，映射
由下表给出：
__________，使不等式
成立的x的集合是_____________.
，使得对定义域
内的任意两个
，均有
成立，则称函数
在定义域
满足利普希茨条件，则常数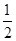
上选择一点C建造垃圾处理厂，其对市区的影响度与所选地 
的图像与函数
的图像所有交点的横坐标之和等于