题目内容
设z1,z2为共轭复数,且(z1+z2)2-3z1•z2i=4-6i,求z1和z2.
解:设z1 =a+bi,a、b∈R,则z2=a-bi.由(z1+z2)2-3z1•z2i=4-6i得,
4a2-3(a2+b2)i=4-6i,∴4a2=4,-3(a2+b2)=-6.
解得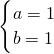 ,或
,或 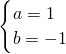 ,或
,或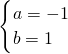 ,或
,或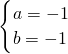 .
.
∴ ,或
,或  ,或
,或  ,或
,或 .
.
分析:设z1 =a+bi,a、b∈R,则z2=a-bi.由条件可得4a2-3(a2+b2)i=4-6i,根据两个复数相等的充要条件可得 4a2=4,-3(a2+b2)=-6,解方程组求出z1和z2 .
点评:本题主要考查复数代数形式的混合运算,两个复数相等的充要条件,求得 4a2=4,-3(a2+b2)=-6,是解题的关键.
4a2-3(a2+b2)i=4-6i,∴4a2=4,-3(a2+b2)=-6.
解得
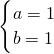 ,或
,或 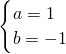 ,或
,或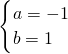 ,或
,或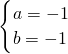 .
.∴
 ,或
,或  ,或
,或  ,或
,或 .
.分析:设z1 =a+bi,a、b∈R,则z2=a-bi.由条件可得4a2-3(a2+b2)i=4-6i,根据两个复数相等的充要条件可得 4a2=4,-3(a2+b2)=-6,解方程组求出z1和z2 .
点评:本题主要考查复数代数形式的混合运算,两个复数相等的充要条件,求得 4a2=4,-3(a2+b2)=-6,是解题的关键.

练习册系列答案
相关题目