题目内容
已知函数f(x)=ax(1)若函数f(x)在其定义域内为单调函数,求实数a的取值范围;
(2)若函数f(x)的图象在x=1处的切线的斜率为0,且an+1=f′(![]() )-nan+1.
)-nan+1.
①若a1≥3,求证:an≥n+2;
②若a1=4,试比较![]() 与
与![]() 的大小,并说明你的理由.
的大小,并说明你的理由.
解:(1)∵f(1)=a-b=0,∴a=b.
∴f′(x)=a+![]() .要使函数f(x)在其定义域内为单调函数,则在(0,+∞)内f′(x)=a+
.要使函数f(x)在其定义域内为单调函数,则在(0,+∞)内f′(x)=a+![]() =
= ![]() 恒大于零,或恒小于零.
恒大于零,或恒小于零.
1° 当a>0时,则有f′(x)=a(![]() )2+a
)2+a![]() >0恒成立,即a
>0恒成立,即a![]() >0,即a>1;
>0,即a>1;
2° 当a<0时,
令t=![]() ,则f′(x)=g(t)=a(t
,则f′(x)=g(t)=a(t![]() )2+a
)2+a![]() 的对称轴为t=
的对称轴为t=![]() <0.
<0.
∴f′(x)=g(t)在(0,+∞)内递减,
∴f′(x)<g(0)=a<0恒成立;
所以当a<0时,有f′(x)=a(![]() )2+a
)2+a![]() <0恒成立.
<0恒成立.
3° 当a=0时,f′(x)=![]() 在(0,+∞)上恒有f′(x)<0.
在(0,+∞)上恒有f′(x)<0.
综合1°、2°、3°可知所求的实数a的取值范围为a>1或a≤0.
(2)∵函数f(x)的图象在x=1处的切线的斜率为0,∴f′(1)=0,即a+a-2=0,解得a=1.
∴f′(x)=(![]() -1)2,
-1)2,
∴an+1=f′(![]() )-nan+1=an2-nan+1.
)-nan+1=an2-nan+1.
①用数学归纳法证明:(i)当n=1时,a1≥3=1+2,不等式成立;(ii)假设当n=k时不等式成立,即ak≥k+2,那么ak-k≥2>0,
∴ak+1=ak(ak-k)+1≥2(k+2)+1=(k+3)+k+2>k+3,这就是说,当n=k+1时,ak+1≥(k+1)+2.根据(i)和(ii),对于所有n≥1,有an≥n+2.
②由an+1=an(an-n)+1及①,对k≥2,有ak=ak-1(ak-1-k+1)+1≥ak-1(k-1+2-k+1)+1=2ak-1+1,
∴ak+1≥2(ak-1+1)≥22(ak-2+1)≥23(ak-3+1)≥…≥2k-1(a1+1).
而![]() ,于是当k≥2时,
,于是当k≥2时,![]() ,
,
∴![]()
=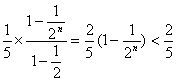 .
.

| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |