题目内容
已知动圆过定点Q(1,0),且与定直线x=-1相切.
(1)求此动圆圆心P的轨迹C的方程;
(2)若过点M(4,0)的直线l与曲线C分别相交于A,B两点,若2
=
,求直线l的方程.
(1)求此动圆圆心P的轨迹C的方程;
(2)若过点M(4,0)的直线l与曲线C分别相交于A,B两点,若2
| AM |
| MB |
分析:(1)利用抛物线的定义即可得出;
(2)设直线AB的方程为:y=k(x-4)(k存在且k≠0),把直线的方程与抛物线的方程联立,利用根与系数的关系及已知向量相等即可得出直线的斜率,进而得出直线的方程.
(2)设直线AB的方程为:y=k(x-4)(k存在且k≠0),把直线的方程与抛物线的方程联立,利用根与系数的关系及已知向量相等即可得出直线的斜率,进而得出直线的方程.
解答: 解:(1)由题意知,动圆圆心M的轨迹C是以定点Q(1,0)为焦点,以定直线
解:(1)由题意知,动圆圆心M的轨迹C是以定点Q(1,0)为焦点,以定直线
x=-1为准线的抛物线,其方程为:y2=4x;
(2)设直线AB的方程为:y=k(x-4)(k存在且k≠0).
联立
,消去x,得 ky2-4y-16k=0,
显然△>0,
设A(x1,y1),B(x2,y2),
则 y1+y2=
,y1y2=-16.
=(4-x1,-y1),
=(x2-4,y2).
又∵2
=
,∴-2y1=y2.
联立
,消去y1,y2得k2=2,解得k=±
.
∴直线l的方程为y=±
(x-4).
 解:(1)由题意知,动圆圆心M的轨迹C是以定点Q(1,0)为焦点,以定直线
解:(1)由题意知,动圆圆心M的轨迹C是以定点Q(1,0)为焦点,以定直线x=-1为准线的抛物线,其方程为:y2=4x;
(2)设直线AB的方程为:y=k(x-4)(k存在且k≠0).
联立
|
显然△>0,
设A(x1,y1),B(x2,y2),
则 y1+y2=
| 4 |
| k |
| AM |
| MB |
又∵2
| AM |
| MB |
联立
|
| 2 |
∴直线l的方程为y=±
| 2 |
点评:熟练掌握抛物线的定义、直线与圆锥曲线相交问题的解题模式、根与系数的关系、向量相等的运用是解题的关键,该题是中档题.

练习册系列答案
相关题目
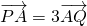 ,求直线l的方程.
,求直线l的方程.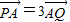 ,求直线l的方程.
,求直线l的方程.