题目内容
正方形中心G为(-6,3),它的一边所在直线方程为5x+12y+7=0,求其它三边所在直线的方程。
答案:
解析:
解析:
设正方形ABCD的边AB所在直线的方程为5x+12y+7=0 ① 因CD∥AB,则设CD所在直线的方程为5x+12y+m=0(m≠7) ② 过中心G作一直线与AB、CD分别交于点(x0,y0),(x1,y1)则
5x1+12y1+m=0 相加得5(x0+x1)+12(y0+y1)+m+7=0 得m=-19,∴CD的方程为5x+12y-19=0,又AD、BC与AB垂直,可设AD、BC所在直线的方程为12x-5y+n=0,得:
12x-5y+74=0,12x-5y+100=0。
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 解得n1=74,n2=100,故BC和AD所在直线为:
解得n1=74,n2=100,故BC和AD所在直线为: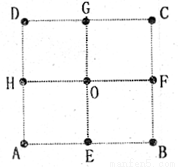 如图,在正方形ABCD中,E、F、G、H是各边中点,O是正方形中心,在A、E、B、F、C、G、D、H、O这九个点中,以其中三个点为顶点作三角形,在这些三角形中,互不全等的三角形共有( )
如图,在正方形ABCD中,E、F、G、H是各边中点,O是正方形中心,在A、E、B、F、C、G、D、H、O这九个点中,以其中三个点为顶点作三角形,在这些三角形中,互不全等的三角形共有( )