题目内容
设数列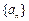 的前
的前 项和为
项和为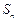 ,其中
,其中 ,
,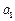 为常数,且
为常数,且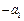 、
、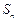 、
、 成等差数列.
成等差数列.
(Ⅰ)求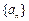 的通项公式;
的通项公式;
(Ⅱ)设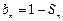 ,问:是否存在
,问:是否存在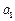 ,使数列
,使数列 为等比数列?若存在,求出
为等比数列?若存在,求出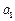 的值;
的值;
若不存在,请说明理由.
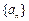 的前
的前 项和为
项和为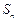 ,其中
,其中 ,
,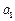 为常数,且
为常数,且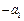 、
、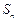 、
、 成等差数列.
成等差数列.(Ⅰ)求
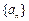 的通项公式;
的通项公式;(Ⅱ)设
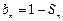 ,问:是否存在
,问:是否存在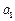 ,使数列
,使数列 为等比数列?若存在,求出
为等比数列?若存在,求出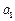 的值;
的值;若不存在,请说明理由.
(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
(Ⅰ)依题意,得 .于是,当
.于是,当 时,有
时,有 .
.
两式相减,得 (
( ).
).
又因为 ,
, ,所以数列
,所以数列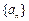 是首项为
是首项为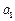 、公比为3的等比数列.
、公比为3的等比数列.
因此, (
( );
);
(Ⅱ)因为 ,所以
,所以 .
.
要使 为等比数列,当且仅当
为等比数列,当且仅当 ,即
,即 .
.
 .于是,当
.于是,当 时,有
时,有 .
.两式相减,得
 (
( ).
).又因为
 ,
, ,所以数列
,所以数列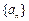 是首项为
是首项为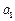 、公比为3的等比数列.
、公比为3的等比数列.因此,
 (
( );
);(Ⅱ)因为
 ,所以
,所以 .
.要使
 为等比数列,当且仅当
为等比数列,当且仅当 ,即
,即 .
.
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
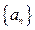 前n项和记为
前n项和记为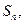
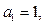
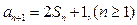 ,
,
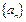 的的通项公式;(Ⅱ)等差数列
的的通项公式;(Ⅱ)等差数列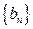 的各项为正,其前n项和为
的各项为正,其前n项和为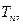 且
且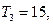 又
又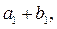
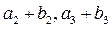 成等比数列,求
成等比数列,求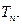
 (n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是
(n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是 ,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q =
,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q = ,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.
,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.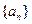 的前
的前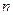 项和为
项和为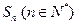 ,关于数列
,关于数列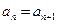 ;
;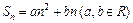 ,则数列
,则数列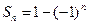 ,则数列
,则数列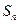 为数列
为数列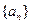 的前
的前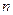 项和,
项和,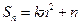 ,
,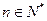 ,其中
,其中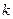 是常数.
是常数.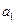 及
及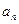 ;
;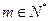 ,
,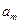 ,
, ,
,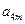 成等比数列,求
成等比数列,求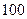 的正整数中,被
的正整数中,被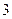 除余
除余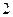 的数的和是 .
的数的和是 .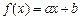 ,其中
,其中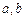 为实数,
为实数,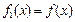 ,
,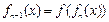 ,
,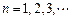 ,若
,若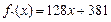 ,则
,则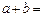 .
.