Question

两个骰子的点数分别为b、c，则方程x²+bx+c=0有两个实根的概率为（ ）
A．
B．
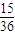
C．
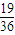
D．

Answer 1

【答案】分析：由题意知本题是一个古典概型，试验发生包含的事件共有36个结果，满足条件的事件是方程有解，则△=b²-4c≥0，整理为b²≥4c，结合这个结论，列举出满足条件的事件数，得到概率．
解答：解：由题意知本题是一个古典概型，
∵试验发生包含的事件共有36个结果，
满足条件的事件是方程有解，则△=b²-4c≥0，∴b²≥4c，
满足条件的数记为（b²，4c），共有（4，4），（9，4），（9，8），（16，4），（16，8），（16，12），
（16，16），（25，4），（25，8），（25，12），（25，16），（25，20），（25，24），
（36，4），（36，8），（36，12），（36，16），（36，20），（36，24），19个结果，
∴方程有两个实根的概率P=．
故选C
点评：本题考查古典概型和一元二次方程的解，是一个综合题，这是经常出现的一个组合，本题的重点实际上不是应用概率公式，而是一元二次方程的解．