Question

椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的左焦点为F，直线x=m与椭圆相交于A，B两点，当△FAB的周长最大时，△FAB的面积为ab．若b=1，则椭圆的准线方程是

 

．

Answer 1

分析：画出图象，结合图象以及椭圆的定义求出△FAB的周长的表达式，求出何时周长最大，可得△FAB的面积为

1

2

×2c×

2b2

a

=ab，结合b=1，求出a，c，即可求出椭圆的准线方程．

解答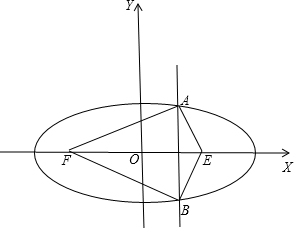：解：设椭圆的右焦点E．如图：
由椭圆的定义得：△FAB的周长为：AB+AF+BF=AB+（2a-AE）+（2a-BE）=4a+AB-AE-BE；
∵AE+BE≥AB；
∴AB-AE-BE≤0，当AB过点E时取等号；
∴△FAB的周长：AB+AF+BF=4a+AB-AE-BE≤4a；
∴△FAB的周长的最大值是4a；
此时，△FAB的面积为

1

2

×2c×

2b2

a

=ab，
∴a²=2bc，
∵b=1，
∴a²=2c，
∴1+c²=2c，
∴c=1，
∴a=

2

，
∴椭圆的准线方程是x=±

a2

c

=±

2

．
故答案为：x=±

2

．

点评：本题考查椭圆的简单性质，考查椭圆的定义．解决本题的关键在于利用定义求出周长的表达式．