题目内容
已知动圆过定点P(1,0),且与定直线l,x=-1相切,点C在l上
(Ⅰ)求动圆圆心的轨迹M的方程;
(Ⅱ)设过点P,且斜率为![]() 的直线与曲线M相交于A、B两点,问△ABC能否为正三角形?若能,求点C的坐标,;若不能,说明理由。
的直线与曲线M相交于A、B两点,问△ABC能否为正三角形?若能,求点C的坐标,;若不能,说明理由。
解:(Ⅰ)解法一曲线M是以点P为焦点,直线l为准线的抛物线,所以曲线M的方程为y2=4x
解法二:设M(x,y),依题意有|MP|=|MN|,所以![]() 化简得:y2=4x
化简得:y2=4x
(Ⅱ)()由题意得,直线AB的方程为![]()
由 消y得
消y得![]()
所以A点坐标为![]()
因此,直线l上不存在点B、C,使得△ABC是正三角形

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.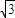 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.