Question

求下列函数的值域:

(1)y=cos²x+2sinx-2；(2)y=.

Answer 1

（1）解：y=cos²x+2sinx-2=-sin²x+2sinx-1=-(sinx-1)².

∵-1≤sinx≤1,

∴sinx-1∈［-2,0］.

∴y∈［-4，0］.

∴函数y=cos²x+2sinx-2的值域是［-4，0］.

（2）解法一：∵y==1+,

∴当sinx=-1时，y_min=1+=.

∴值域为［,+∞).

解法二：由y=,得sinx=.

又∵-1≤sinx≤1,

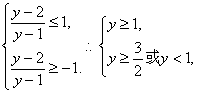∴∴y≥.

∴函数y=的值域为［,+∞).

温馨提示

（1）一般函数的值域求法有：观察法、配方法、判别式法、反比例函数法等，而三角函数是函数的特殊形式，用上述方法时，要注意三角函数的特性.

（2）求三角函数的值域，主要是运用sinx,cosx的有界性，以及复合函数的有关性质.