题目内容
在等比数列 {an} 中, 则
则 =( )
=( )
| A.2 | B. | C.2或 | D.-2 或 - |
C
解析试题分析:因为 所以
所以 ,所以
,所以 ,
, 。
。
考点:等比数列的性质;等比数列的通项公式。
点评:熟练应用等比数列的性质: 。
。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若等比数列的首项为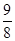 ,末项为
,末项为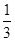 ,公比为
,公比为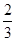 ,则这个数列的项数为( )
,则这个数列的项数为( )
| A.3 | B.4 | C.5 | D.6 |
设等比数列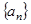 中,前n项和为
中,前n项和为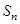 ,已知
,已知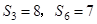 ,则
,则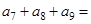
A. | B.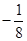 | C.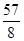 | D.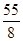 |
设等比数列 中,前n项和为
中,前n项和为 ,已知
,已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
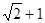 与
与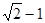 ,两数的等比中项是( )
,两数的等比中项是( )
A.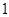 | B.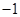 | C.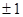 | D.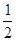 |
在等比数列{an}中, =1,
=1, =3,则
=3,则 的值是
的值是
| A.14 | B.16 | C.18 | D.20 |
数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为( )
| A.2n-n-1 | B.2n+1-n-2 |
| C.2n | D.2n+1-n |
 中,每 行 中 的 三 个 数 成 等 差 数 列,且
中,每 行 中 的 三 个 数 成 等 差 数 列,且 、
、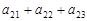 、
、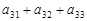 成等比数列,下列四个判断正确的有 (A )
成等比数列,下列四个判断正确的有 (A )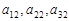 必成等比数列 ②第1列
必成等比数列 ②第1列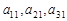 不一定成等比数列
不一定成等比数列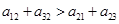 ④若9个数之和等于9,则
④若9个数之和等于9,则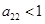
 的左右焦点分别为
的左右焦点分别为 ,P是椭圆上的一点,且
,P是椭圆上的一点,且 成等比数列,则椭圆的离心率的取值范围为( )
成等比数列,则椭圆的离心率的取值范围为( )


