题目内容
设 的定义域为D,若
的定义域为D,若 满足条件:存在
满足条件:存在 ,使
,使 在
在 上的值域是
上的值域是 ,则称
,则称 为“倍缩函数”.若函数
为“倍缩函数”.若函数 为“倍缩函数”,则t的范围是( )
为“倍缩函数”,则t的范围是( )
A. | B. | C. | D.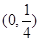 |
D
解析试题分析:因为函数 在其定义域上是增函数,且函数
在其定义域上是增函数,且函数 为“倍缩函数”,且
为“倍缩函数”,且 在
在 上的值域是
上的值域是 ,所以
,所以 ,即
,即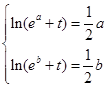 ,所以方程
,所以方程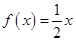 必有两个不等的实数根。解
必有两个不等的实数根。解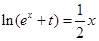 得
得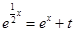 ,整理可得
,整理可得 。令
。令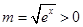 ,则上式可变形为
,则上式可变形为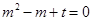 。所以方程
。所以方程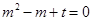 在
在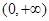 有两个不等的实数根,所以
有两个不等的实数根,所以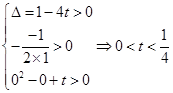 。故D正确。
。故D正确。
考点:1函数的定义域和值域;2函数的单调性;3指数和对数的互化;4二次函数的图像和性质。

练习册系列答案
相关题目
定义域为R的函数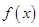 满足
满足 ,当
,当 时,
时,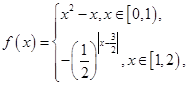 则当
则当 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
已知函数 的值域是
的值域是 ,则实数
,则实数 的取值范围是 ( )
的取值范围是 ( )
A. ; ; | B. ; ; | C. ; ; | D. . . |
.对于函数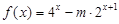 ,若存在实数
,若存在实数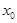 ,使得
,使得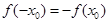 成立,则实数
成立,则实数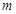 的取值范围是( )
的取值范围是( )
A.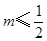 | B.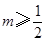 | C.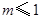 | D.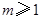 |
一次函数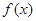 的图象过点
的图象过点 和
和 ,则下列各点在函数
,则下列各点在函数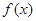 的图象上的是( )
的图象上的是( )
A. | B. | C. | D. |
由表格中的数据可以判定方程 的一个零点所在的区间是
的一个零点所在的区间是 ,则
,则 的值为( )
的值为( )
 | -1 | 0 | 1 | 2 | 3 |
 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
 | 1 | 2 | 3 | 4 | 5 |
已知 为偶函数,当
为偶函数,当 时,
时, ,满足
,满足 的实数
的实数 的个数为( )
的个数为( )
| A.2 | B.4 | C.6 | D.8 |
若函数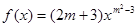 是幂函数,则
是幂函数,则 的值为( )
的值为( )
A.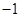 | B. | C.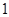 | D.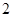 |
函数y=log2 的图象( )
的图象( )
| A.关于原点对称 | B.关于直线y=-x对称 |
| C.关于y轴对称 | D.关于直线y=x对称 |