题目内容
已知函数 ,x∈R,若f(α)=-2,f(β)=2,且|α-β|的最小值等于
,x∈R,若f(α)=-2,f(β)=2,且|α-β|的最小值等于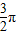 ,则正数ω的值为 ;函数f(x)的单调递减区间为 .
,则正数ω的值为 ;函数f(x)的单调递减区间为 .
【答案】分析:根据题意得到|α-β|的最小值是半个周期,然后根据周期的计算公式可得ω,进而得到函数的解析式,即可求出函数的单调减区间.
解答:解:由题意可得:f(α)=-2,f(β)=2,且|α-β|的最小值等于 ,
,
所以函数 的正周期T=3π.
的正周期T=3π.
又因为 ,所以ω=
,所以ω= .
.
所以 ,
,
所以函数f(x)的单调递减区间为[ +3kπ,
+3kπ, ].
].
故答案为: ,[
,[ +3kπ,
+3kπ, ].
].
点评:解决此类问题的关键是熟练掌握三角函数的性质,即单调性、周期性、奇偶性以及函数的图象.
解答:解:由题意可得:f(α)=-2,f(β)=2,且|α-β|的最小值等于
 ,
,所以函数
 的正周期T=3π.
的正周期T=3π.又因为
 ,所以ω=
,所以ω= .
.所以
 ,
,所以函数f(x)的单调递减区间为[
 +3kπ,
+3kπ, ].
].故答案为:
 ,[
,[ +3kπ,
+3kπ, ].
].点评:解决此类问题的关键是熟练掌握三角函数的性质,即单调性、周期性、奇偶性以及函数的图象.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 ,x∈R,若f(α)=-2,f(β)=2,且|α-β|的最小值等于
,x∈R,若f(α)=-2,f(β)=2,且|α-β|的最小值等于 ,则正数ω的值为________;函数f(x)的单调递减区间为________.
,则正数ω的值为________;函数f(x)的单调递减区间为________.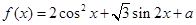 (x∈R).
(x∈R).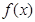 有最大值2,求实数a的值;⑵求函数
有最大值2,求实数a的值;⑵求函数