题目内容
已知f(x)是定义在[-e,0)∪(0,e]上的奇函数,且当x∈(0,e]时,f(x)=ax+lnx.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)是否存在实数a<0,使得当x∈[-e,0)时,函数f(x)的最小值是3?
解:(Ⅰ)设x∈[-e,0),则-x∈(0,e],故f(-x)=-ax+ln(-x).
又f(x)是定义在[-e,0)∪(0,e]上的奇函数,∴-f(x)=-ax+ln(-x),
∴f(x)=ax-ln(-x),故f(x)=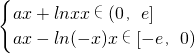 .
.
(Ⅱ)假设存在实数a<0,使得当x∈[-e,0)时,函数f(x)的最小值是3,
则由f′(x)=a- =
=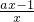 知,
知,
①当 ≤-e,即-
≤-e,即- ≤a<0时,由x∈[-e,0)得f′(x)≥0,故f(x)=ax-ln(-x)是[-e,0)上的增函数,
≤a<0时,由x∈[-e,0)得f′(x)≥0,故f(x)=ax-ln(-x)是[-e,0)上的增函数,
故f(x)的最小值为f(-e)=-ae-1=3,解得 a=-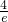 <-
<- (舍去).
(舍去).
②当x∈(0,e],即a<- ,则有当x∈[-e,
,则有当x∈[-e, )时,f′(x)<0,f(x)单调递减;
)时,f′(x)<0,f(x)单调递减;
当x∈( ,0)时,f′(x)>0,f(x)单调递增,f(x)的最小值等于 f(
,0)时,f′(x)>0,f(x)单调递增,f(x)的最小值等于 f( )=1-ln(-
)=1-ln(- )=3,
)=3,
解得 a=-e2.
综上,存在实数a=-e2,似的当x∈[-e,0)时,函数f(x)的最小值是3.
分析:(Ⅰ)设x∈[-e,0),则-x∈(0,e],故f(-x)=-ax+ln(-x),根据函数的奇偶性求出此时的解析式,即可得到函数在定义域内的解析式.
(Ⅱ)假设存在实数a<0,满足条件,①当 ≤-e,即-
≤-e,即- ≤a<0时,利用单调性球的函数的最小值,a值不存在,②当x∈(0,e],即a<-
≤a<0时,利用单调性球的函数的最小值,a值不存在,②当x∈(0,e],即a<- ,利用单调性球的函数的最小值,解出 a=-e2.
,利用单调性球的函数的最小值,解出 a=-e2.
点评:本题考查对数函数的单调性和特殊点,函数的奇偶性,利用导数研究函数得最值,体现了分类讨论的数学思想,确定函数的最小值,是解题的难点和关键.
又f(x)是定义在[-e,0)∪(0,e]上的奇函数,∴-f(x)=-ax+ln(-x),
∴f(x)=ax-ln(-x),故f(x)=
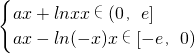 .
.(Ⅱ)假设存在实数a<0,使得当x∈[-e,0)时,函数f(x)的最小值是3,
则由f′(x)=a-
 =
=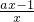 知,
知,①当
 ≤-e,即-
≤-e,即- ≤a<0时,由x∈[-e,0)得f′(x)≥0,故f(x)=ax-ln(-x)是[-e,0)上的增函数,
≤a<0时,由x∈[-e,0)得f′(x)≥0,故f(x)=ax-ln(-x)是[-e,0)上的增函数,故f(x)的最小值为f(-e)=-ae-1=3,解得 a=-
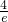 <-
<- (舍去).
(舍去).②当x∈(0,e],即a<-
 ,则有当x∈[-e,
,则有当x∈[-e, )时,f′(x)<0,f(x)单调递减;
)时,f′(x)<0,f(x)单调递减;当x∈(
 ,0)时,f′(x)>0,f(x)单调递增,f(x)的最小值等于 f(
,0)时,f′(x)>0,f(x)单调递增,f(x)的最小值等于 f( )=1-ln(-
)=1-ln(- )=3,
)=3,解得 a=-e2.
综上,存在实数a=-e2,似的当x∈[-e,0)时,函数f(x)的最小值是3.
分析:(Ⅰ)设x∈[-e,0),则-x∈(0,e],故f(-x)=-ax+ln(-x),根据函数的奇偶性求出此时的解析式,即可得到函数在定义域内的解析式.
(Ⅱ)假设存在实数a<0,满足条件,①当
 ≤-e,即-
≤-e,即- ≤a<0时,利用单调性球的函数的最小值,a值不存在,②当x∈(0,e],即a<-
≤a<0时,利用单调性球的函数的最小值,a值不存在,②当x∈(0,e],即a<- ,利用单调性球的函数的最小值,解出 a=-e2.
,利用单调性球的函数的最小值,解出 a=-e2.点评:本题考查对数函数的单调性和特殊点,函数的奇偶性,利用导数研究函数得最值,体现了分类讨论的数学思想,确定函数的最小值,是解题的难点和关键.

练习册系列答案
相关题目