题目内容
已知函数f(x)=ln(1+x)-x(Ⅰ)求f(x)的单调区间;
(Ⅱ)记f(x)在区间[0,n](n∈N*)上的最小值为bx令an=ln(1+n)-bx.
(Ⅲ)如果对一切n,不等式![]() 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
(Ⅳ)求证:![]()
本小题主要考查函数的单调性、最值、不等式、数列等基本知识,考查运用导数研究函数性质的方法,考查分析问题和解决问题的能力.
解法一:
(I)因为f(x)=ln(1+x)-x,所以函数定义域为(-1,+![]() ),且
),且![]() =
=![]() -1=
-1=![]() .
.
由![]() >0得-1<x<0,f(x)的单调递增区间为(-1,0);
>0得-1<x<0,f(x)的单调递增区间为(-1,0);
由![]() <0得x>0,f(x)的单调递增区间为(0,+
<0得x>0,f(x)的单调递增区间为(0,+![]() ).
).
(II)因为f(x)在[0,n]上是减函数,所以bn=f(n)=ln(1+n)-n,
则an=ln(1+n)-bn=ln(1+n)-ln(1+n)+n=n.
(i)![]()
![]()
> ![]()
又![]()
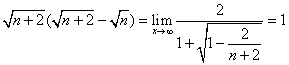 ,
,
因此c<1,即实数c的取值范围是(-![]() ,1].
,1].
(II)由(i)知![]()
因为[![]() ]2
]2
=![]() .
.
所以![]() <
<![]() <
<![]() -
-![]() (n
(n![]() N*),
N*),
则![]() <
<
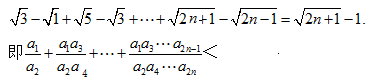
![]() N*)解法二:
N*)解法二:
(Ⅰ)同解法一.
(Ⅱ)因为f(x)在![]() 上是减函数,所以
上是减函数,所以![]()
则![]()
(i)因为![]() 对n∈N*恒成立.所以
对n∈N*恒成立.所以![]() 对n∈N*恒成立.
对n∈N*恒成立.
则![]() 对n∈N*恒成立.
对n∈N*恒成立.
设![]() n∈N*,则c<g(n)对n∈N*恒成立.
n∈N*,则c<g(n)对n∈N*恒成立.
考虑![]()
因为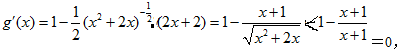
所以![]() 内是减函数;则当n∈N*时,g(n)随n的增大而减小,
内是减函数;则当n∈N*时,g(n)随n的增大而减小,
又因为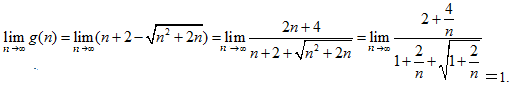
所以对一切![]() 因此c≤1,即实数c的取值范围是(-∞,1].
因此c≤1,即实数c的取值范围是(-∞,1].
(ⅱ) 由(ⅰ)知![]()
下面用数学归纳法证明不等式![]() <
<![]() ( n∈N*).
( n∈N*).
①当n=1时,左边=![]() ,右边=
,右边=![]() ,左边<右边.不等式成立.
,左边<右边.不等式成立.
②假设当n=k时,不等式成立.即![]()
当n=k+1时,![]()
=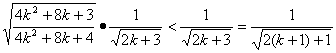
即n=k+1时,不等式成立
综合①、②得,不等式![]() 成立.
成立.
所以![]()
![]() <
<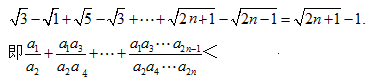
![]() N*).
N*).

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目