题目内容
已知函数 为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为
为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为 的最小值为π,则( )
的最小值为π,则( )
A.ω=2,θ= | B.ω=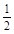 ,θ= ,θ= |
C.ω=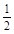 ,θ= ,θ= | D.ω=2,θ= |
A
解析试题分析:由已知条件可知,函数与y=2的
交点的横坐标为 的最小值为π,那么说明了函数的周期为
的最小值为π,那么说明了函数的周期为 ,同时且三角函数为偶函数,则说明了
,同时且三角函数为偶函数,则说明了 ,由于0<θ<π,因此可知
,由于0<θ<π,因此可知 故选A
故选A
考点:本试题考查了三角函数的图形与性质。
点评:函数的图像直观的体现了函数的 性质,因此在解决三角函数周期等问题时,我们往往构造函数,利用函数的图像解题,体现了数形结合法的运用。属于中档题。

练习册系列答案
相关题目
下列式子正确的是 ( )
A. | B. |
C. | D. |
 ,则
,则
A. | B. | C. | D. |
已知 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
已知实系数一元二次方程 的两个实根为
的两个实根为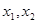 ,且
,且  ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
函数 满足
满足 ,且
,且 ,
, ,则下列等式不成立的是( )
,则下列等式不成立的是( )
A. | B. |
C. | D. |
设函数
 、
、 的零点分别为
的零点分别为 ,则( )
,则( )
A. | B. | C. | D. |
 )x的图象只可能是( )
)x的图象只可能是( )
 的图象大致是( )
的图象大致是( )


