题目内容
3.双曲线的中心在原点,一条渐近性方程为2x-3y=0,一个焦点坐标为($\sqrt{13}$,0),求该双曲线的标准方程.分析 设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,由一条渐近性方程为2x-3y=0,一个焦点坐标为($\sqrt{13}$,0),解方程组求得a2,b2的值.
解答 解:设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,由题意得 c=$\sqrt{13}$=$\sqrt{{a}^{2}+{b}^{2}}$ ①,$\frac{b}{a}=\frac{3}{2}$ ②,
由 ①②得 a2=4,b2=9,
故所求的双曲线方程$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}=1$.
点评 本题考查利用待定系数法求双曲线的标准方程的方法,以及双曲线的简单性质得应用.

练习册系列答案
相关题目
18.在△ABC中,a、b、c分别是角A、B、C的对边,已知b2=c(b+2c),若a=$\sqrt{6}$,cosA=$\frac{7}{8}$,则△ABC的面积等于( )
| A. | $\sqrt{17}$ | B. | $\sqrt{15}$ | C. | $\frac{\sqrt{15}}{2}$ | D. | 3 |
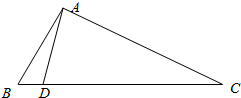 如图,在△ABC中,已知点D在BC边上,AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3.
如图,在△ABC中,已知点D在BC边上,AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3.