题目内容
在△ABC中,cos2| A |
| 2 |
| b+c |
| 2c |
| 9 |
| 10 |
分析:把c的值代入已知的等式求出b的值,然后利用二倍角的余弦函数公式化简已知等式,表示出cosA,再利用余弦定理表示出cosA,两者相等,化简后得到a2+b2=c2,根据勾股定理的逆定理可得三角形ABC为直角三角形,由b和c的值,利用勾股定理求出a的值,然后利用周长的一半即可求出三角形内切圆的半径.
解答:解:∵c=5,
=
,∴b=4,
又cos2
=
=
,
∴cosA=
,
由余弦定理得cosA=
,
则
=
,
∴b2+c2-a2=2b2,即a2+b2=c2,
∴△ABC是以角C为直角的三角形,
根据勾股定理得a=
=3,
则△ABC的内切圆半径r=
(a+b+c)=1.
| b+c |
| 2c |
| 9 |
| 10 |
又cos2
| A |
| 2 |
| 1+cosA |
| 2 |
| b+c |
| 2c |
∴cosA=
| b |
| c |
由余弦定理得cosA=
| b2+c2-a2 |
| 2bc |
则
| b2+c2-a2 |
| 2bc |
| b |
| c |
∴b2+c2-a2=2b2,即a2+b2=c2,
∴△ABC是以角C为直角的三角形,
根据勾股定理得a=
| c2-b2 |
则△ABC的内切圆半径r=
| 1 |
| 2 |
点评:此题属于解三角形的题型,涉及的知识有二倍角的余弦函数公式,余弦定理,以及勾股定理和逆定理,解此类题往往根据定理及公式建立已知与未知之间的联系,从而求出三角形中未知的量,达到解三角形的目的,化简已知的等式表示出cosA是本题的突破点,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
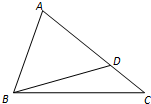 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=