题目内容
平面直角坐标系中,O为坐标原点,已知两点A(3,1)、B(-1,3),若点C满足A.3x+2y-11=0 B.(x-1)2+(y-2)2=5
C.2x-y=0 D.x+2y-5=0
解析:设![]() =(x,y),
=(x,y),![]() =(3,1),
=(3,1),![]() =(-1,3),
=(-1,3),
α![]() =(3α,α),β
=(3α,α),β![]() =(-β,3β),
=(-β,3β),
又α![]() +β
+β![]() =(3α-β,α+3β),
=(3α-β,α+3β),
∴(x,y)=(3α-β,α+3β).
∴![]()
①-②×3-10β=x-3y③
②+①×3,10α=3x+y④
④-③,结合α+β=1,因此可得x+2y=5.
答案:D

练习册系列答案
相关题目
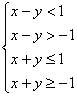 ,则点P的轨迹表示的平面区域为( )
,则点P的轨迹表示的平面区域为( )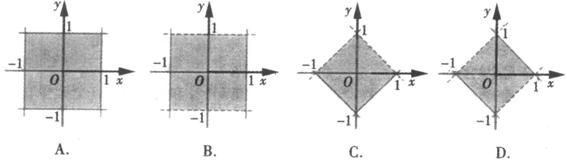
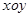 中O是坐标原点,
中O是坐标原点,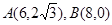 ,圆
,圆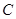 是
是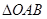 的外接圆,过点(2,6)的直线为
的外接圆,过点(2,6)的直线为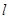 。
。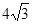 ,求直线
,求直线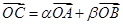 ,其中α,β∈R,且α+β=1,则点C的轨迹方程为
,其中α,β∈R,且α+β=1,则点C的轨迹方程为