题目内容
15.解不等式:4x2-2x<25.分析 把不等式4x2-2x<25化为4x2-2x-25<0,求出对应方程4x2-2x-25=0的两个实数根,写出该不等式的解集.
解答 解:不等式4x2-2x<25可化为
4x2-2x-25<0,
∵△=(-2)2-4×4×(-25)=404>0,
∴对应方程4x2-2x-25=0的两个实数解为
x1=$\frac{1+\sqrt{101}}{4}$,x2=$\frac{1-\sqrt{101}}{4}$;
∴该不等式的解集为{x|$\frac{1-\sqrt{101}}{4}$<x<$\frac{1+\sqrt{101}}{4}$}.
点评 本题考查了一元二次不等式的解法与应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.某学校开设“蓝天工程博览课程”,组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆,每个年级任选一个博物馆参观,则有且只有两个年级选择甲博物馆的方案有( )
| A. | $A_6^2×A_5^4$种 | B. | $A_6^2×{5^4}$种 | C. | $C_6^2×A_5^4$种 | D. | $C_6^2×{5^4}$种 |
 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数 的图象,若函数
的图象,若函数 在区间
在区间 和
和 上均单调递增,则实数
上均单调递增,则实数 的取值范围是( )
的取值范围是( ) B.
B.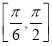
 D.
D.

 B.
B.
 D.
D.
 是虚数单位,若复数
是虚数单位,若复数 在复平面内对应的点在第四象限,则实数
在复平面内对应的点在第四象限,则实数 的值可以是( )
的值可以是( ) ,则
,则 等于( )
等于( ) B.
B.
 D.
D.
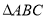 中,
中, ,若
,若 为
为 的值为( )
的值为( )