题目内容
已知点P是以F1,F2为焦点的椭圆 上一点,且
上一点,且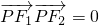 ,
, ,则该椭圆的离心率等于________.
,则该椭圆的离心率等于________.

分析:依题意,焦点三角形PF1F2为直角三角形,利用解直角三角形知识可得|PF2|=
 c,再由椭圆定义,可得|PF2|=
c,再由椭圆定义,可得|PF2|= ,从而由等式
,从而由等式 =
= c求得椭圆离心率
c求得椭圆离心率解答:在三角形PF1F2中,|F1F2|=2c,
∵
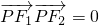 ,∴∠F1PF2=90°
,∴∠F1PF2=90°∵
 ,∴|PF1|=2|PF2|
,∴|PF1|=2|PF2|∴|F1F2|2=|PF1|2+|PF2|2=5|PF2|2=4c2,
∴|PF2|=
 c
c∵|PF1|+|PF2|=3|PF2|=2a
∴|PF2|=

∴
 =
= c
c∴e=
 =
=
故答案为

点评:本题考查了椭圆的几何性质,椭圆中焦点三角形的性质和计算,椭圆定义的应用及椭圆离心率的定义及计算方法,有一定的运算量

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似三角形,则称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比.已知椭圆C1
的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似三角形,则称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比.已知椭圆C1 以抛物线
以抛物线 的焦点为一个焦点,且椭圆上任意一点到两焦点的距离之和为4.(1)若椭圆C2与椭圆C1相似,且相似比为2,求椭圆C2的方程.
的焦点为一个焦点,且椭圆上任意一点到两焦点的距离之和为4.(1)若椭圆C2与椭圆C1相似,且相似比为2,求椭圆C2的方程. 异于原点的交点,证明点Q一定落在双曲线4x2-4y2=1上.
异于原点的交点,证明点Q一定落在双曲线4x2-4y2=1上.