题目内容
x<0,当x=| 3 | x |
分析:由题意利用基本不等式求出-2x-
的最小值,并求出取最小知时的x的值,再求出y的最小值.
| 3 |
| x |
解答:解:∵x<0,∴-2x>0,-
>0,
由基本不等式得,-2x-
≥2
,当且仅当2x=
时取等号,
即x=±
,由x<0得,x=-
;
∴当x=-
时,y有最小值4+2
.
故答案为:-
,4+2
.
| 3 |
| x |
由基本不等式得,-2x-
| 3 |
| x |
| 6 |
| 3 |
| x |
即x=±
| ||
| 2 |
| ||
| 2 |
∴当x=-
| ||
| 2 |
| 6 |
故答案为:-
| ||
| 2 |
| 6 |
点评:本题考查了利用基本不等式求函数的最小值,注意三个条件即:一正二定三相等.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 ax2+bx(a>0),且f′(1)=0
ax2+bx(a>0),且f′(1)=0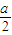 )-1
)-1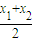 时,则称AB存在“中值相依切线”.请问在函数f(x)的图象上是否存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由.
时,则称AB存在“中值相依切线”.请问在函数f(x)的图象上是否存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由. 的最小值________.
的最小值________.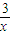 的最小值 .
的最小值 .