题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{ax+a,x≥0}\\{{e}^{ax},x<0}\end{array}\right.$为R上的增函数,则实数a的取值范围是( )| A. | (0,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (1,+∞) |
分析 若f(x)=$\left\{\begin{array}{l}{ax+a,x≥0}\\{{e}^{ax},x<0}\end{array}\right.$为R上的增函数,根据第一、二段函数为增函数,且x=0时,第一段的函数值不小于第二段的函数值,进而构造关于a的不等式组,解不等式组可得实数a的取值范围.
解答 解:∵f(x)=$\left\{\begin{array}{l}{ax+a,x≥0}\\{{e}^{ax},x<0}\end{array}\right.$为R上的增函数,
∴$\left\{\begin{array}{l}{a>1}\\{a≥{e}^{0}}\end{array}\right.$,
解得:a>1,
故实数a的取值范围为[1,+∞),
故选:B.
点评 题考查的知识点是分段函数的单调性,其中根据已知构造关于a的不等式组,是解答的关键.

练习册系列答案
相关题目
11.已知三个力f1,f2,f3作用于物体同一点,使物体处于平衡状态,若f1=(2,2),f2=(-2,3).则|f3|为 ( )
| A. | 2.5 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 5 |
1.若P是正四面体V-ABC的侧面VBC上一点,点P到平面ABC的距离与到点V的距离相等,则动点P的轨迹为( )
| A. | 一条线段 | B. | 椭圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
8.存在最小的合数n,使得2n-1≡1(modn)成立,则n的值为( )
| A. | 327 | B. | 341 | C. | 331 | D. | 355 |
6.设$\overrightarrow{a}$、$\overrightarrow{b}$都是非零向量,下列四个条件中,使$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$=$\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$成立的充要条件是( )
| A. | $\overrightarrow{a}$=-$\overrightarrow{b}$ | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$且方向相同 | C. | $\overrightarrow{a}$=2$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$且|$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
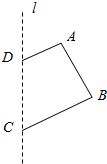 如图,直角梯形ABCD中,AB⊥BC,绕着CD所在直线l旋转,指出所得到的几何体的结构特征.
如图,直角梯形ABCD中,AB⊥BC,绕着CD所在直线l旋转,指出所得到的几何体的结构特征.