题目内容
(本小题满分12分)已知二次函数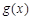 对任意实数x都满足
对任意实数x都满足
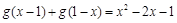 ,且
,且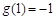 .令
.令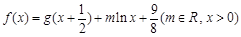 .
.
(1)求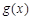 的表达式;
的表达式;
(2)设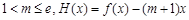 ,证明:对任意
,证明:对任意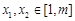 ,恒有
,恒有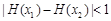 .
.
【答案】
解:(1) 设
∴
∴ 
又 ∵ ,则
,则
∴  ················································································ 5分
················································································ 5分
(2) ∵ 对
∴  在[1,m]内单调递减
在[1,m]内单调递减
于是
 ······························· 8分
······························· 8分
记 ,则
,则

∴ 函数 在
在 是单调增函数
是单调增函数
∴ 
∴ 命题成立··························································································· 12分
【解析】略

练习册系列答案
相关题目