题目内容
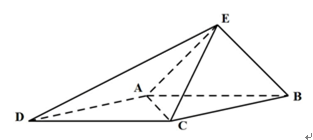
如图,在长方体 中,
中, 点
点 在棱
在棱 上.
上.
(1)求异面直线 与
与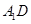 所成的角;
所成的角;
(2)若二面角 的大小为
的大小为 ,求点
,求点 到面
到面 的距离.
的距离.
(1)对于异面直线的所成的角,一般采用平移法,平移到一个三角形中,借助于余弦定理求解。
(2)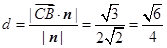
解析试题分析:解法一:(1)连结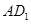 .由
.由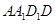 是正方形知
是正方形知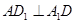 .
.
∵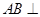 平面
平面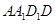 ,
,
∴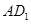 是
是 在平面
在平面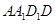 内的射影.
内的射影.
根据三垂线定理得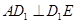 ,
,
则异面直线 与
与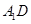 所成的角为
所成的角为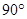 . 5分
. 5分
(2)作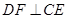 ,垂足为
,垂足为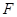 ,连结
,连结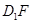 ,则
,则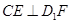 .
.
所以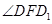 为二面角
为二面角 的平面角,
的平面角,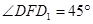 .于是
.于是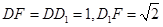 ,
,
易得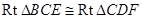 ,所以
,所以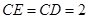 ,又
,又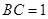 ,所以
,所以 .
.
设点 到平面
到平面 的距离为
的距离为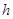 ,则由于
,则由于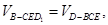 即
即 ,
,
因此有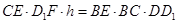 ,即
,即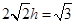 ,∴
,∴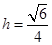 .…………12分
.…………12分
解法二:如图,分别以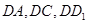 为
为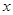 轴,
轴,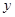 轴,
轴,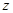 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.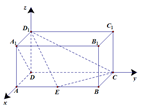
(1)由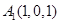 ,得
,得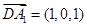 ,
,
设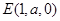 ,又
,又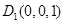 ,则
,则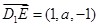 .
.
∵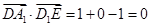 ∴
∴ ,则异面直线
,则异面直线 与
与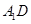 所成的角为
所成的角为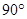 . 5分
. 5分
(2)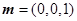 为面
为面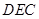 的法向量,设
的法向量,设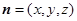 为面
为面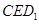 的法向量,则
的法向量,则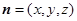
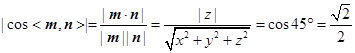 ,
,
∴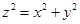 . ①
. ①
由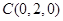 ,得
,得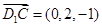 ,则
,则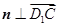 ,即
,即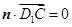 ,∴
,∴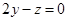
②由①、②,可取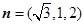 ,又
,又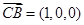 ,
,
所以点 到平面
到平面 的距离
的距离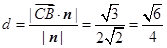 . 12分
. 12分
考点:异面直线所成的角,点到面的距离
点评:考查了异面直线所成的角以及点到面的距离的求解,属于基础题。

练习册系列答案
相关题目
 为平行四边形,
为平行四边形,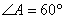 ,
,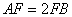 ,
,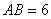 ,点
,点 在
在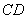 上,
上,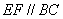 ,
,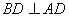 ,
,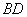 与
与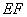 相交于
相交于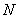 .现将四边形
.现将四边形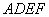 沿
沿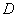 在平面
在平面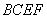 上的射影恰在直线
上的射影恰在直线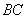 上.
上.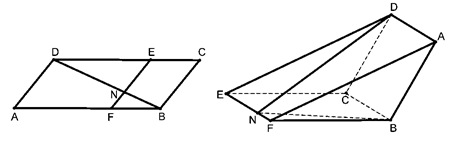
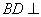 平面
平面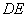 与平面
与平面 的正方体
的正方体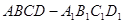 中,
中,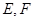 分别为
分别为 的中点.
的中点.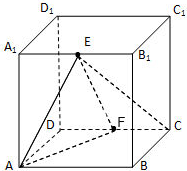
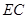 与平面
与平面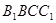 所 成 角的大小;
所 成 角的大小;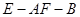 的大小.
的大小.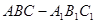 中,
中,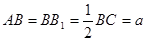 ,
,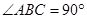 ,
,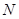 、
、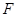 分别为
分别为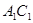 、
、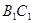 的中点.
的中点.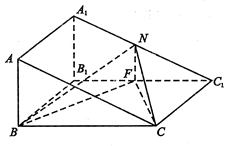
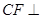 平面
平面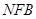 ;
;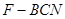 的体积.
的体积. 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.
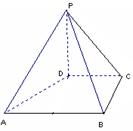
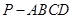 的底面是正方形,
的底面是正方形,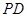 ⊥底面
⊥底面 ,点
,点 在棱
在棱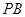 上.
上.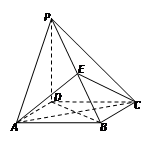
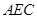 ⊥平面
⊥平面 ;
;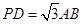 且
且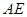 与平面
与平面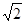
 中,
中, ,
, ,
, ,
, ,
, , 点
, 点 ,
, 分别在棱
分别在棱 上,且
上,且 ,
,
 平面PAC
平面PAC 的中点时,求
的中点时,求 与平面
与平面 所成的角的正弦值;
所成的角的正弦值; 为直二面角?并说明理由.
为直二面角?并说明理由.