题目内容
已知a∈R,函数f(x)=-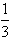 x3+
x3+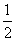 ax2+2ax(x∈R),
ax2+2ax(x∈R),
(1)当a=1时,求函数f(x)的单调递增区间;
(2)函数f(x)是否在R上单调递减,若是,求出a的取值范围;若不是,请说明理由;
(3)若函数f(x)在[-1,1]上单调递增,求a的取值范围。
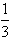 x3+
x3+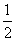 ax2+2ax(x∈R),
ax2+2ax(x∈R), (1)当a=1时,求函数f(x)的单调递增区间;
(2)函数f(x)是否在R上单调递减,若是,求出a的取值范围;若不是,请说明理由;
(3)若函数f(x)在[-1,1]上单调递增,求a的取值范围。
解:(1)当a=1时,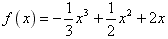 ,
,
∴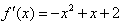 ,
,
令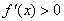 ,即
,即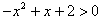 ,
,
即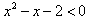 ,解得-1<x<2,
,解得-1<x<2,
∴函数f(x)的单调递增区间是(-1,2);
(2)若函数f(x)在R上单调递减,则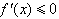 对x∈R都成立,
对x∈R都成立,
即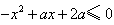 对x∈R都成立,即
对x∈R都成立,即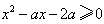 对x∈R都成立,
对x∈R都成立,
∴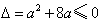 ,解得
,解得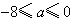 ,
,
∴当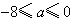 时,函数f(x)在R上单调递减;
时,函数f(x)在R上单调递减;
(3)∵函数f(x)在[-1,1]上单调递增,
∴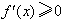 对x∈[-1,1]都成立,
对x∈[-1,1]都成立,
∴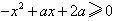 对x∈[-1,1]都成立,即
对x∈[-1,1]都成立,即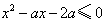 对x∈[-1,1]都成立,
对x∈[-1,1]都成立,
令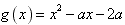 ,
,
则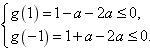 ,解得
,解得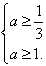 ,
,
∴a≥1。
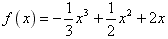 ,
,∴
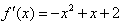 ,
,令
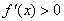 ,即
,即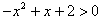 ,
,即
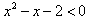 ,解得-1<x<2,
,解得-1<x<2,∴函数f(x)的单调递增区间是(-1,2);
(2)若函数f(x)在R上单调递减,则
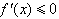 对x∈R都成立,
对x∈R都成立,即
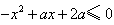 对x∈R都成立,即
对x∈R都成立,即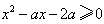 对x∈R都成立,
对x∈R都成立,∴
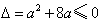 ,解得
,解得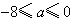 ,
,∴当
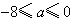 时,函数f(x)在R上单调递减;
时,函数f(x)在R上单调递减;(3)∵函数f(x)在[-1,1]上单调递增,
∴
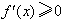 对x∈[-1,1]都成立,
对x∈[-1,1]都成立,∴
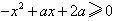 对x∈[-1,1]都成立,即
对x∈[-1,1]都成立,即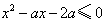 对x∈[-1,1]都成立,
对x∈[-1,1]都成立,令
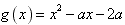 ,
,则
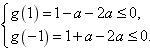 ,解得
,解得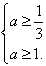 ,
,∴a≥1。

练习册系列答案
相关题目