题目内容
(本小题满分12分)设函数![]() .
.
(1)当方程![]() =0只有一个实数解时,求实数
=0只有一个实数解时,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 且当
且当![]() 时,恒有
时,恒有![]() 求实数
求实数![]() 的取值范围.
的取值范围.


解:(Ⅰ)![]()

![]() 方程
方程![]() 只有一个实数解,
只有一个实数解,![]() 没有实数解.
没有实数解.
![]()
![]() ,解得
,解得![]() .
.
所以,当方程![]() 只有一个实数解时,实数
只有一个实数解时,实数![]() 的取值范围是
的取值范围是![]() ……………4分
……………4分
(Ⅱ)由![]() ……………5分
……………5分
因为![]()
![]() 在
在![]() 和
和![]() 内单调递减,
内单调递减,
在![]() 内单调递增. ……………7分
内单调递增. ……………7分
(1)当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]()
![]() 无解. ………………9分
无解. ………………9分
(2)当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
![]()
![]() =
=![]()
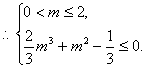 解得
解得![]() ………………11分
………………11分
综上所述,![]() 的取值范围为
的取值范围为![]() ………………12分
………………12分

练习册系列答案
相关题目