题目内容
设|z|=1且z≠±i,证明
分析:(1)z为复数可设出z=x+yi(x、y∈R),再进行运算、判断;(2)由|z|=1转为z![]() =1,即
=1,即![]() =
=![]() ,进一步化简.
,进一步化简.
证法一:设z=x+yi(x、y∈R).
则![]() =
=![]()
=![]()
=![]() .
.
∵|z|=1,∴x2+y2=1.
∴y-x2y-y3=y(1-x2-y2)=0.
∴![]() ∈R.
∈R.
证法二:∵|z|=1,∴z![]() =1.∴
=1.∴![]() =
=![]() .
.
∴![]() =
=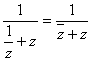 .
.
设z=a+bi,则z+![]() =2a∈R.
=2a∈R.
∴![]() 为实数.
为实数.

练习册系列答案
相关题目
题目内容
设|z|=1且z≠±i,证明
分析:(1)z为复数可设出z=x+yi(x、y∈R),再进行运算、判断;(2)由|z|=1转为z![]() =1,即
=1,即![]() =
=![]() ,进一步化简.
,进一步化简.
证法一:设z=x+yi(x、y∈R).
则![]() =
=![]()
=![]()
=![]() .
.
∵|z|=1,∴x2+y2=1.
∴y-x2y-y3=y(1-x2-y2)=0.
∴![]() ∈R.
∈R.
证法二:∵|z|=1,∴z![]() =1.∴
=1.∴![]() =
=![]() .
.
∴![]() =
=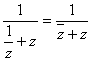 .
.
设z=a+bi,则z+![]() =2a∈R.
=2a∈R.
∴![]() 为实数.
为实数.
