Question

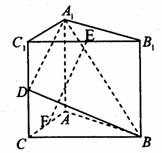
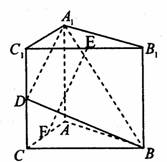
如下图，在直三棱柱ABC—A₁B₁C₁中，∠ACB=90°,BC=CC₁=a,AC=2a.

(1)求证:AB₁⊥BC₁;

(2)求二面角B—AB₁—C的大小；

(3)求点A₁到平面AB₁C的距离.

Answer 1

(1)证明:

∵ABC—A₁B₁C₁是直三棱柱,∴CC₁⊥平面ABC.∴AC⊥CC₁.∵AC⊥BC,∴AC⊥平面B₁BCC₁.

∴B₁C是AB₁在平面B₁BCC₁上的射影.

∵BC=CC₁,∴四边形B₁BCC₁是正方形.∴BC₁⊥B₁C.

    根据三垂线定理,得AB₁⊥BC₁.

(2)解:设BC₁∩B₁C=O,作OP⊥AB₁于点P，连结BP.

∵BO⊥AC,且BO⊥B₁C,

∴BO⊥平面AB₁C.

∴OP是BP在平面AB₁C上的射影.

    根据三垂线定理,得AB₁⊥BP.

∴∠OPB是二面角B—AB₁—C的平面角.

∵△OPB₁∽△ACB₁,∴.

∴OP==a.

    在Rt△POB中，tan∠OPB==,

∴二面角B—AB₁—C的大小为arctan.

(3)解法一:∵A₁C₁∥AC,A₁C₁平面AB₁C,

∴A₁C₁∥平面AB₁C.

∴点A₁到平面AB₁C的距离与点C₁到平面AB₁C的距离相等.

∵BC₁⊥平面AB₁C,

∴线段C₁O的长度为点A₁到平面AB₁C的距离.

∴点A₁到平面AB₁C的距离为C₁O=a.

解法二:连结A₁C,有=,设点A₁到平面AB₁C的距离为h.

∵B₁C₁⊥平面ACC₁A₁,

∴·h=·B₁C₁.

    又=AC·B₁C=a²,

=AC·A₁A=a²,∴h==a.

∴点A₁到平面AB₁C的距离为a.