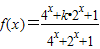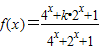题目内容
已知函数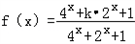
(1)若对于任意的x∈R,f(x)>0恒成立,求实数k的取值范围;
(2)若f(x)的最小值为﹣3,求实数k的取值范围;
(3)若对于任意的x1、x2、x3,均存在以f(x1)、f(x2)、f(x3)为三边长的三角形,求实数k 的取值范围.
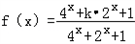
(1)若对于任意的x∈R,f(x)>0恒成立,求实数k的取值范围;
(2)若f(x)的最小值为﹣3,求实数k的取值范围;
(3)若对于任意的x1、x2、x3,均存在以f(x1)、f(x2)、f(x3)为三边长的三角形,求实数k 的取值范围.
解:(1)设t=2x,则y=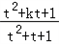 (t>0),
(t>0),
∵y>0恒成立,
∴t>0时,t2+kt+1>0恒成立,即t>0时,k>﹣(t+ )恒成立,
)恒成立,
∵t>0时,t+ ≥2,
≥2,
∴﹣(t+ )≤﹣2,
)≤﹣2,
当t= ,即t=1时,﹣(t+
,即t=1时,﹣(t+ )有最大值为﹣2,
)有最大值为﹣2,
∴k>﹣2;
(2)f(x)=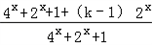 =1+
=1+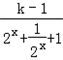 ,
,
令t=2x+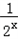 +1≥3,则y=1+
+1≥3,则y=1+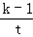 (t≥3),
(t≥3),
当k﹣1>0,即k>1时,y∈(1,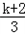 ],无最小值,舍去;
],无最小值,舍去;
当k﹣1=0,即k=1时,y∈{1},最小值不是﹣3,舍去;
当k﹣1<0,即k<1时,y∈[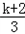 ,1),最小值为
,1),最小值为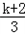 =﹣3得k=﹣11;
=﹣3得k=﹣11;
综上k=﹣11.
(3)因对任意实数x1、x2、x3,都存在以f(x1)、f(x2)、f(x3)为三边长的三角形,
故f(x1)+f(x2)>f(x3)
对任意的x1、x2、x3∈R恒成立.
当k>1时,
∵2<f(x1)+f(x2)≤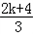 且1<f(x3)≤
且1<f(x3)≤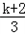 ,
,
故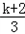 ≤2,
≤2,
∴1<k≤4;
当k=1时,
∵f(x1)=f(x2)=f(x3)=1,满足条件;
当k<1时,
∵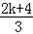 ≤f(x1)+f(x2)<2,且
≤f(x1)+f(x2)<2,且 ≤f(x3)<1,
≤f(x3)<1,
故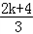 ≥1,
≥1,
∴﹣ ≤k<1;
≤k<1;
综上所述:﹣ ≤k≤4.
≤k≤4.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
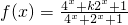
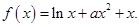
 在
在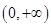 是增函数,求
是增函数,求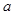 的取值范围;
的取值范围;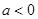 ,对于函数
,对于函数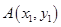 ,
,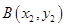 ,其中
,其中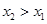 ,直线
,直线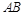 的斜率为
的斜率为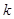 ,记
,记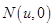 ,若
,若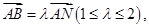 求证:
求证: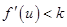 .
.