题目内容
(1)已知矩阵 ,
, .在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到的曲线F,求曲线F的方程.
.在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到的曲线F,求曲线F的方程.(2)在极坐标系中,已知圆C的圆心坐标为C (2,
 ),半径R=
),半径R= ,求圆C的极坐标方程.
,求圆C的极坐标方程.(3)已知a,b为正数,求证:
 .
.
【答案】分析:(1)利用矩阵的乘法法则求出MN,设出已知直线的一点坐标(x,y),求出这点在矩阵MN对应变换下的坐标(x',y')与设出坐标
(x,y)的关系,分别求出x′和y′,代入已知直线方程即可得到曲线F的方程;
(2)将圆心极坐标化为普通坐标,根据半径写出圆的标准方程,然后令x等于ρcosθ,y等于ρsinθ,代入化简即可得到圆C的极坐标方程;(3)由a与b都为正数,给不等式的左边乘以(a+b),去括号化简后,利用基本不等式求出最小值,然后把不等式变形即可得证.
解答:解:(1)由题设得 ,
,
设(x,y)是直线2x-y+1=0上任意一点,
点(x,y)在矩阵MN对应的变换作用下变为(x',y'),
则有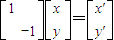 ,即
,即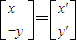 ,所以
,所以
因为点(x,y)在直线2x-y+1=0上,从而2x'-(-y')+1=0,即:2x'+y'+1=0
所以曲线F的方程为2x+y+1=0;
(2)将圆心C(2,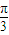 )化成直角坐标为(1,
)化成直角坐标为(1,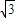 ),半径R=
),半径R=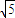 ,
,
故圆C的方程为(x-1)2+(y-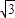 )2=5.
)2=5.
再将C化成极坐标方程,得(ρcosθ-1)2+(ρcosθ-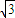 )2=5.
)2=5.
化简,得ρ2-4ρcos(θ-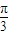 )+1=0,此即为所求的圆C的方程;
)+1=0,此即为所求的圆C的方程;
(3)证明:∵a>0,b>0,所以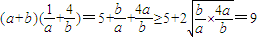
∴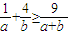
点评:此题考查学生会求一点在矩阵变换下的坐标,会根据条件求圆的极坐标方程,灵活运用基本不等式化简求值,是一道综合题.
(x,y)的关系,分别求出x′和y′,代入已知直线方程即可得到曲线F的方程;
(2)将圆心极坐标化为普通坐标,根据半径写出圆的标准方程,然后令x等于ρcosθ,y等于ρsinθ,代入化简即可得到圆C的极坐标方程;(3)由a与b都为正数,给不等式的左边乘以(a+b),去括号化简后,利用基本不等式求出最小值,然后把不等式变形即可得证.
解答:解:(1)由题设得
 ,
,设(x,y)是直线2x-y+1=0上任意一点,
点(x,y)在矩阵MN对应的变换作用下变为(x',y'),
则有
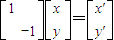 ,即
,即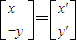 ,所以
,所以
因为点(x,y)在直线2x-y+1=0上,从而2x'-(-y')+1=0,即:2x'+y'+1=0
所以曲线F的方程为2x+y+1=0;
(2)将圆心C(2,
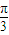 )化成直角坐标为(1,
)化成直角坐标为(1,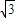 ),半径R=
),半径R=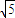 ,
,故圆C的方程为(x-1)2+(y-
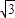 )2=5.
)2=5.再将C化成极坐标方程,得(ρcosθ-1)2+(ρcosθ-
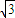 )2=5.
)2=5.化简,得ρ2-4ρcos(θ-
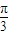 )+1=0,此即为所求的圆C的方程;
)+1=0,此即为所求的圆C的方程;(3)证明:∵a>0,b>0,所以
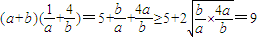
∴
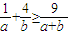
点评:此题考查学生会求一点在矩阵变换下的坐标,会根据条件求圆的极坐标方程,灵活运用基本不等式化简求值,是一道综合题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目