题目内容
1．
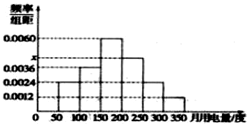利用简单随机抽样从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到350度之间，频率分布直方图如图所示．在这些用户中，用电量落在区间[150，250]内的户数为（ ）| A． | 46 | B． | 48 | C． | 50 | D． | 52 |
分析 根据频率分布直方图，利用频率、频数与样本容量的关系进行解答即可．
解答 解：这些用户中，用电量落在区间[150，250]内的频率为
1-（0.0024+0.0036+0.0024+0.0012）×50=0.52
∴用电量落在区间[150，250]内的户数为
100×0.52=52．
故选：D．
点评 本题考查了频率分布直方图的应用问题，也考查了频率=$\frac{频数}{样本容量}$的应用问题，是基础题目．
练习册系列答案
相关题目
11．执行如图所示的程序，输出的S为（ ）
| A． | -1006 | B． | 1007 | C． | -1008 | D． | 1009 |
12．
在篮球比赛中，某篮球队队员投进三分球的个数如表所示：
如图是统计上述6名队员在比赛中投进的三分球总数s的程序
框图，则图中的判断框内应填入的条件是（ ）
在篮球比赛中，某篮球队队员投进三分球的个数如表所示：| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数ai | a1 | a2 | a3 | a4 | a5 | a6 |
框图，则图中的判断框内应填入的条件是（ ）
| A． | i＜6 | B． | i＜7 | C． | i＜8 | D． | i＜9 |
9．设集合U={1，2，3，4}，A={1，2}，B={2，4}，则B∩（∁UA）=（ ）
| A． | {2} | B． | {4} | C． | {1，2，4} | D． | {1，4} |
如图，在四棱锥P-ABCD中，PC⊥底面ABCD．底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2，AD=CD=1，E是线段PB的中点．
6．双曲线${y^2}-\frac{x^2}{m}=1$的离心率$e=\sqrt{3}$，则以双曲线的两条渐近线与抛物线y2=mx的交点为顶点的三角形的面积为（ ）
| A． | $4\sqrt{2}$ | B． | $12\sqrt{2}$ | C． | $8\sqrt{2}$ | D． | $16\sqrt{2}$ |
如图，在三棱锥S-ABC中，SA⊥底面ABC，AC=AB=SA=2，AC⊥AB，D，E分别是AC，BC的中点，F在SE上，且SF=2FE．
6．圆x2+y2=4被直线$\sqrt{3}x+y-2\sqrt{3}$=0截得的弦长为（ ）
| A． | $2\sqrt{3}$ | B． | $2\sqrt{2}$ | C． | 3 | D． | 2 |