题目内容
在△ABC中,角A、B、C所对的边长分别为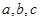 ,若角C=120°,
,若角C=120°,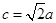 ,则( )
,则( )
A.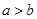 B.
B.
C.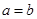 D.
D.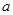 与
与 的大小关系不能确定
的大小关系不能确定
A
解析试题分析:∵∠C=120°,c=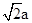 ∴由余弦定理可知c2=a2+b2-2abcosC,∴a2-b2=ab,a-b=
∴由余弦定理可知c2=a2+b2-2abcosC,∴a2-b2=ab,a-b=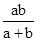 ∵a>0,b>0,∴a-b=
∵a>0,b>0,∴a-b=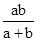
∴a>b,故选A
考点:本试题主要考查了解三角形的运用。考查余弦定理,特殊角的三角函数值,不等式的性质,比较法,属中档题.
点评:解决该试题的关键是由余弦定理可知c2=a2+b2-2abcosC,进而求得a-b=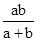 >0,判断出a>b.
>0,判断出a>b.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
原点和点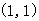 在直线
在直线 的两侧,则
的两侧,则 的取值范围是( )
的取值范围是( )
A. 或 或 | B. 或 或 |
C. | D. |
已知 , 若
, 若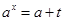 ,则
,则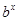 与
与 的大小关系为
的大小关系为
A.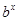 > > | B.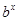 = = | C.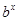 < < | D.不能确定 |
已知实数 、
、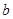 、
、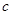 满足
满足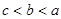 ,且
,且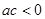 ,那么下列不等式一定成立的是
,那么下列不等式一定成立的是
A.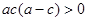 | B.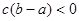 | C.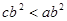 | D.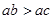 |
与“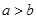 ”等价的不等式是( )
”等价的不等式是( )
A.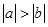 | B.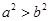 | C.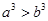 | D.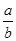 >1 >1 |
已知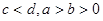 , 则下列不等式中一定成立的是
, 则下列不等式中一定成立的是
A.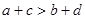 | B.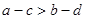 | C.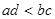 | D.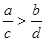 |
当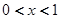 时,则下列大小关系正确的是( )
时,则下列大小关系正确的是( )
A. | B.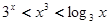 |
C.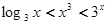 | D.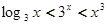 |
已知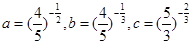 则
则 的大小关系( )
的大小关系( )
A.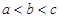 | B.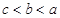 |
C.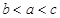 | D.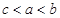 |
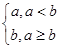 已知a=30.3,b=0.33,c=log30.3,则(a*b)*c=______(用a,b,c作答).
已知a=30.3,b=0.33,c=log30.3,则(a*b)*c=______(用a,b,c作答).