题目内容
(本小题满分12分)
已知斜三棱柱ABC—A1B1C1的底面是正三角形,侧面ABB1A1是菱形,且 ,M是A1B1的中点,
,M是A1B1的中点,
(1)求证: 平面ABC;
平面ABC;
(2)求二面角A1—BB1—C的余弦值。

【答案】
(Ⅰ)∵侧面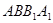 是菱形且
是菱形且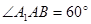 ∴
∴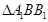 为正三角形
为正三角形
又∵点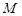 为
为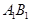 的中点
∴
的中点
∴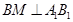
∵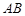 ∥
∥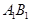 ∴
∴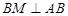
由已知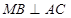 ∴
∴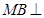 平面
平面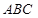 (4分)
(4分)
(Ⅱ)(法一)连接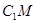 ,作
,作 于
于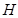 ,连接
,连接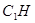
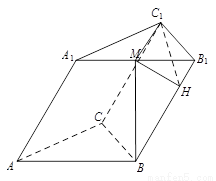
由(Ⅰ)知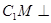 面
面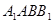 ,∴
,∴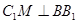
又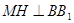 ∴
∴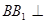 面
面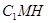 ∴
∴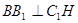
∴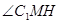 为所求二面角的平面角
(8分)
为所求二面角的平面角
(8分)
设菱形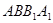 边长为2,则
边长为2,则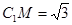
在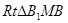 中,由
中,由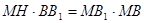 知:
知: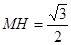
在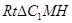 中,
中, 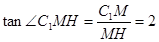 ∴
∴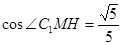
即二面角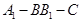 的余弦值为
的余弦值为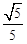 (12分)
(12分)
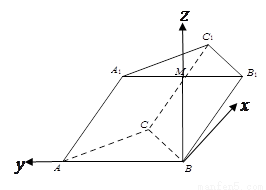
(法二)如图建立空间直角坐标系
设菱形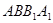 边长为2
边长为2
得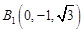 ,
,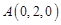
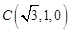 ,
,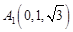
则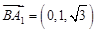 ,
,
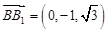 ,
,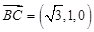
设面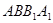 的法向量
的法向量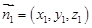 ,由
,由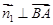 ,
,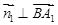 得
得
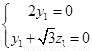 ,令
,令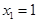 ,得
,得 (8分)
(8分)
设面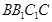 的法向量
的法向量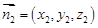 ,
由
,
由 ,
,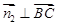 得
得
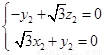 ,令
,令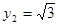 ,得
,得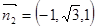 (10分)
(10分)
得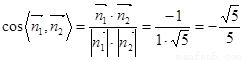 .
.
又二面角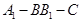 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为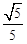 (12分)
(12分)
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目