题目内容
(本小题满分12分)
已知数列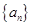 的首项为2,点
的首项为2,点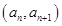 在函数
在函数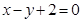 的图像上
的图像上
(Ⅰ)求数列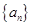 的通项公式;
的通项公式;
(Ⅱ)设数列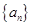 的前
的前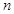 项之和为
项之和为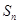 ,求
,求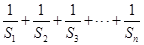 的值.
的值.
已知数列
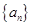 的首项为2,点
的首项为2,点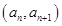 在函数
在函数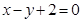 的图像上
的图像上(Ⅰ)求数列
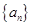 的通项公式;
的通项公式;(Ⅱ)设数列
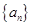 的前
的前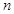 项之和为
项之和为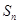 ,求
,求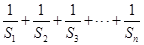 的值.
的值.解(I) 点
点 在函数
在函数 的图象上,
的图象上, ·· 2分
·· 2分
 数列
数列 是以首项为2公差为2的等差数列,·············· 4分
是以首项为2公差为2的等差数列,·············· 4分
 ························ 6分
························ 6分
(Ⅱ) ···················· 8分
···················· 8分
 ,······················· 9分
,······················· 9分
 ········ 10分
········ 10分
 ----------------------------- 12分
----------------------------- 12分
 点
点 在函数
在函数 的图象上,
的图象上, ·· 2分
·· 2分 数列
数列 是以首项为2公差为2的等差数列,·············· 4分
是以首项为2公差为2的等差数列,·············· 4分 ························ 6分
························ 6分(Ⅱ)
 ···················· 8分
···················· 8分  ,······················· 9分
,······················· 9分 ········ 10分
········ 10分 ----------------------------- 12分
----------------------------- 12分试题分析:(I)将(an,an+1)代入f(x)=x+2,利用等差数列的定义即可证明数列{an}是等差数列,可求其通项公式;
(II)利用等差数列的前n项和公式得到
 ,进而裂项法求解前n项和公。
,进而裂项法求解前n项和公。点评:解决该试题的关键先理解等差数列定义得到其通项公式,然后裂项法得到求和。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 中,
中, ,
, (
( ),数列
),数列 项和为
项和为 。(1)证明:数列
。(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 。
。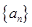 满足:
满足: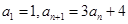 ;
;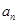 ;
;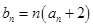 ,求数列
,求数列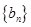 的前
的前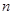 项和为
项和为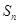 。
。
 …
… .
. :
: ,
, ,
, ,
, ,…,那么数列
,…,那么数列 =
= 前n项和为_____ _ _ ___。
前n项和为_____ _ _ ___。 中,
中, ,
, 是方程
是方程 的两个根,则数列
的两个根,则数列 前
前 项和
项和 ( )
( )



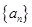 的前
的前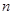 项和
项和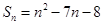 ,
,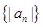 的前
的前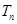 .
. 的前n项和Tn.
的前n项和Tn. 的前
的前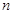 项和
项和 ____________.
____________.